Apéndice B

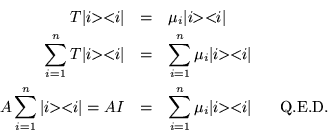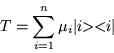
De las hipótesis de completamiento, introducida en la teoría se sigue un teorema conocido como ``Teorema Spectral'', el cual nos dice que toda matriz arbitraria que tenga un conjunto completo de eigenvectores, se puede expresar como el producto de sus eigenvalores por los productos exteriores de sus eigenvectores, esto es:

$$T=\sum_{i=1}^n \mu_i \vert i \!\! > < \!\! i\vert$$

Demostración:

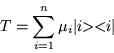
Partiendo de la ecuación de eigenvalores para $T$, es decir:

$$T\vert i \!\! > = \mu_i\vert i \!\! >$$

multiplicando por la derecha por el eigenvector renglón $< \!\! i\vert$

$$\begin{eqnarray*} T\vert i \!\! >< \!\! i\vert & = & \mu_i \vert i \!\! >< \!\!... ...i \!\! >< \!\! i\vert \mbox{\hspace{.2in} Q.E.D.\hspace{.2in}} \end{eqnarray*}$$