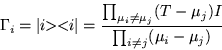
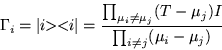
Una forma de calcular estos operadores idempotentes, es
recordando que si ![]() es una matriz que se puede diagonalizar,
entonces es posible expresarla como:
es una matriz que se puede diagonalizar,
entonces es posible expresarla como:
En donde ![]() es una matriz cuyas columnas son los eigenvectores
de la matriz
es una matriz cuyas columnas son los eigenvectores
de la matriz ![]() y
y ![]() es una matriz diagonal, cuyos elementos
son los eigenvalores de
es una matriz diagonal, cuyos elementos
son los eigenvalores de ![]() .
.
Restemos ![]() en ambos miembros de B.1.
en ambos miembros de B.1.
Con objeto de poder visualizar bien esto calculamos los
productos parciales.
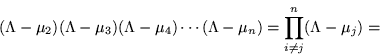
![\begin{displaymath}
\left[\begin{array}{ccccc}
\mu_1-\mu_2 & & & & \\ & 0 & & ...
... & & \\ & & & \ddots & \\ & & & & \
\end{array}\right]\times
\end{displaymath}](img1024.gif)
![\begin{displaymath}
\left[\begin{array}{ccccc}
\mu_1-\mu_4 & & & & \\ & \mu_2-...
...-\mu_n & & \\ & & & \ddots & \\ & & & & 0
\end{array}\right]
\end{displaymath}](img1025.gif)
![\begin{displaymath}
=\left[\begin{array}{cccccccc}
(\mu_1-\mu_2) & (\mu_1-\mu...
... & & & & & & \ddots & \\
& & & & & & & 0 \end{array}\right]
\end{displaymath}](img1026.gif)
![\begin{displaymath}
\prod_{i\neq j}^n (\Lambda -\mu_j) =\prod_{j\neq 1}^n (\mu_...
...y}\right]
=\prod_{j\neq 1}^n (\mu_1-\mu_j) :1 \!\!><\!\! 1:
\end{displaymath}](img1027.gif)
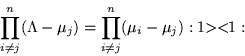
Por otra parte si multiplicamos la ecuación (B.2) por
la izquierda y derecha respectivamente, resulta:
Analicemos el producto de ![]() por el vector ordenado
por el vector ordenado ![]()
![\begin{displaymath}
u:i \!\!> =(\vert 1 \!\! >\vert 2 \!\! >\cdots\vert i \!\! ...
...{array}{c} 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \end{array}\right]
\end{displaymath}](img1033.gif)
Del cálculo de este producto vemos que, como ![]() consta de
columnas que son los eigenvectores, multiplicada por un vector, el
cual tiene un ``uno'' en el lugar
consta de
columnas que son los eigenvectores, multiplicada por un vector, el
cual tiene un ``uno'' en el lugar ![]() -ésimo y ``ceros'' en los
demás lugares, el resultado de este producto, selecciona
precisamente la columna
-ésimo y ``ceros'' en los
demás lugares, el resultado de este producto, selecciona
precisamente la columna ![]() -ésima de la matriz
-ésima de la matriz ![]() , por lo tanto:
, por lo tanto:
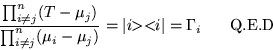
Analizando esta fórmula vemos entre otras cosas, que cuando
hay factores repetidos, es necesario omitir el eigenvalor que hace que
los factores sean cero ya que si no lo hacemos ![]() , lo que
implica que el producto exterior de los eigenvectores sería cero,
por el momento consideramos eigenvalores distintos, y el producto de
índices distintos nos da eigenvalores distintos.
, lo que
implica que el producto exterior de los eigenvectores sería cero,
por el momento consideramos eigenvalores distintos, y el producto de
índices distintos nos da eigenvalores distintos.