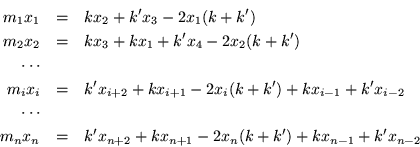
Obtención de la matriz de movimiento para la cadena diatómica. Para el caso de interacciones a segundos vecinos, las ecuaciones de movimiento están dadas por:
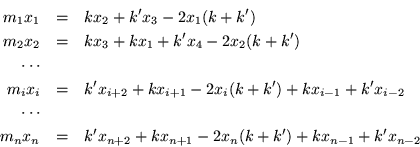
En donde ![]() es una matriz pentadiagonal de la forma
es una matriz pentadiagonal de la forma
![\begin{displaymath}
K = \left[\begin{array}{ccccccc}
a_0 & a_1 & a_2 & & & & \...
...dots & \ddots & \ddots & \ddots & \ddots
\end{array}\right]
\end{displaymath}](img1184.gif)
Por otra parte como nos interesa que la matriz de movimiento
para el caso de una cadena diatómica resulte simétrica, ya que en
esta forma los cálculos numéricos se facilitan bastante, entonces
para lograrlo es conveniente definir la transformación
En donde la matriz
![]() resulta ser
completamente simétrica, esto es, supongamos que
resulta ser
completamente simétrica, esto es, supongamos que
![]() es
una matriz diagonal de la forma
es
una matriz diagonal de la forma
![\begin{displaymath}
\sqrt{M}^{\;-1} =\left[\begin{array}{cccccc}
\frac{1}{\sq...
...
\vdots & & & & & \\
0 & & & & \ddots & \end{array}\right]
\end{displaymath}](img1194.gif)
![\begin{displaymath}
\left[\begin{array}{ccccc}
\frac{1}{\sqrt{M}} & & & & \\ ...
...frac{1}{\sqrt{M}} & & \\
& & & & \ddots \end{array}\right] =
\end{displaymath}](img1195.gif)
![\begin{displaymath}
=\left[\begin{array}{ccccccc}
\frac{a_0}{m} & \frac{a_1}{\...
...dots & & & & & & \vdots \\
0 & & & & & & \end{array}\right]
\end{displaymath}](img1196.gif)
Que es finalmente la matriz de movimiento de una cadena lineal de masas alternantes con interacciones a segundos vecinos.