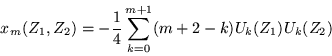| (E.1) |
Los eigenvalores que dan las frecuencias de los modos normales, para
la vibración de una cadena, con interacciones a segundos vecinos y
con ambos extremos fijos están determinados por los ceros de:
| (E.1) |
Sin embargo, para simplificar el álgebra, transformamos más
esta expresión. Es conveniente ignorar el denominador ![]() ,
y llamar al determinante principal
,
y llamar al determinante principal ![]() ; además es claro
que
; además es claro
que ![]() es siempre divisible por
es siempre divisible por ![]() , desde luego que sus
elementos son diferencia de polinomios idénticos en
, desde luego que sus
elementos son diferencia de polinomios idénticos en ![]() y
y ![]() .
Por lo tanto
.
Por lo tanto
![]() y una diferencia de sus
y una diferencia de sus ![]() -ésimas potencias es siempre divisible
por
-ésimas potencias es siempre divisible
por ![]() , (incluyendo
, (incluyendo ![]() ), como cada una de las dos columnas
producen tales factores, entonces el determinante como un todo es
divisible por su cuadrado.
), como cada una de las dos columnas
producen tales factores, entonces el determinante como un todo es
divisible por su cuadrado.
Entonces
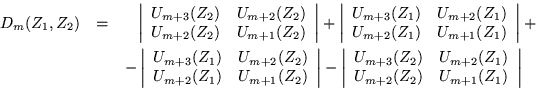
![\begin{eqnarray*}
U_{m+3}(Z)U_{m+1}(Z) & = & \frac{1}{2(Z^2-1)} [T_{2m+6}(Z)-T_...
...m+2}(Z)U_{m+2}(Z) & = & \frac{1}{2(Z^2-1)} [T_{2m+6}(Z)-T_0(Z)]
\end{eqnarray*}](img1146.gif)

Por lo tanto cada uno de los determinantes de la primera
línea tiene el valor ![]() entonces
entonces
Que es una relación de recursión para ![]() , pero es
necesario evaluar explicítamente el determinante que ocurre en
él, esto es:
, pero es
necesario evaluar explicítamente el determinante que ocurre en
él, esto es:
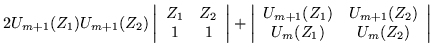 |
|||
| (E.7) |
Puesto que
![]() , resulta que las
condiciones terminales de
, resulta que las
condiciones terminales de ![]() son.
son.
Donde ![]() es conocida como fórmula de
Christoffel-Darboux (ref. [16]). Por lo consiguiente podemos
encontrar de (E.6) que
es conocida como fórmula de
Christoffel-Darboux (ref. [16]). Por lo consiguiente podemos
encontrar de (E.6) que
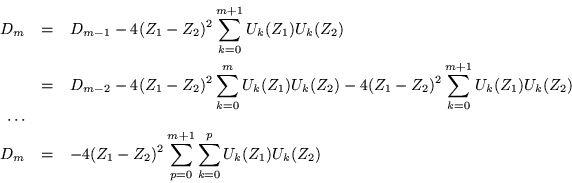
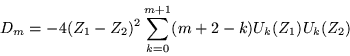
Como nosotros estamos interesados en
![]() ,
entonces el polinomio característico está finalmente dado por:
,
entonces el polinomio característico está finalmente dado por: