Forma recursiva de la ecuación característica.

Debido a que el modelo da lugar a una restricción para los elementos de la matriz $M$, ya que las bandas diagonales son truncadas por las condiciones a la frontera de la cadena, es conveniente introducir coordenadas auxiliares ficticias a las cuales se les impone la condición de que sus desplazamientos sean siempre cero, físicamente equivale a que estén en reposo; para el caso que estamos tratando de interacciones a segundos vecinos, tenemos que suponer dos partículas ficticias en cada extremo, o sea las condiciones suplementarias también llamadas condiciones a la frontera son:

$$\begin{array}{rl} \protect\begin{array}{lcc} x_{n+2} & = ... ...1} & = & 0 \end{array} & \mbox{Extremo izquierdo} \end{array}$$ (2.11)

Como las ecuaciones (2.3') y (2,5') tienen la misma apariencia de (2.4'), entonces podemos escribir (2.4') empleando la ecuación (2.10) en la forma de una relación de recurrencia, esto es:

$$\frac{d^2 x_i}{dt^2} =\lambda x_i =a_i x_{i+1} +a_2 x_{i+2} +a_1 x_{i-1} +a_2 x_{i-2} +a_0 x_i \ .$$

Que es conveniente ponerlo en la forma siguiente:

$$x_{i+2} =-\frac{a_1}{a_2} x_{i+1} +\frac{\lambda -a_0}{a_2} x_i +\frac{a_1}{a_2} x_{i-1} +x_{i-2}$$

y que junto con el siguiente sistema de ecuaciones redundantes:

$$\begin{eqnarray*} x_{i+1} & = & x_{i+1} \\ x_i & = & x_i \\ x_{i-2} & = & x_{i-2} \end{eqnarray*}$$

nos permite construir el sistema matricial de recurrencia siguiente:

$$\left[\begin{array}{l} x_{i+2} \\ x_{i+1} \\ x_i \\ x_{i-1} ... ...ay}{l} x_{i+1} \\ x_i \\ x_{i-1} \\ x_{i-2} \end{array}\right]$$ (2.12)

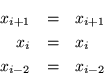
Con el objeto de simplificar el álgebra introduzcamos la siguiente notación

$$T=\left[\begin{array}{cccc} \alpha & \beta & \gamma & \de... ...ay}{l} x_{i+2} \\ x_{i+1} \\ x_i \\ x_{i-1} \end{array}\right]$$

En donde al mismo tiempo, hemos definido:

$$\alpha = \gamma = -\frac{a_1}{a_2} \mbox{\hspace{.2in},\hsp... ...da -a_0}{a_2} \mbox{\hspace{.2in}y\hspace{.2in}} \delta = -1$$ (2.13)