Matriz de transferencia.

Con estas definiciones, el sistema (2.12) se reduce a la forma compacta siguiente:

$$Z_i = T Z_{i-1}$$ (2.14)

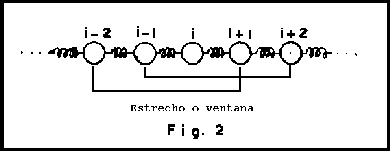
Es precisamente esta matriz de coeficientes, la que es llamada matriz de transferencia [7], ya que nos permite estudiar la variación en el espacio de un segmento, formado por un grupo determinado de partículas, en términos de otro similar, es decir, para el caso que estamos tratando de interacciones a segundos vecinos, podemos estudiar un segmento formado por cuatro desplazamientos que empiezan en la partícula $i+2$ en términos de un segmento similar que empieza desde la partícula $i+1$ gráficamente.

Desarrollando para algunas $i$'s en la ecuación (2.14) tenemos:

$$\mbox{\hspace{.2in}Si\hspace{.2in}} i=1 \mbox{\hspace{.2in}entonces\hspace{.2in}} Z_1 = TZ_0$$

$$\mbox{\hspace{.2in}Si\hspace{.2in}} i=2 \mbox{\hspace{.2in}entonces\hspace{.2in}} Z_2 = TZ_1 = T^2 Z_0$$

$$\ldots$$

$$\mbox{\hspace{.2in}Si\hspace{.2in}} i=n \mbox{\hspace{.2in}entonces\hspace{.2in}} Z_n = T^n Z_0$$ (2.15)

En donde

$$Z_0 = \left[\begin{array}{l} x_2 \\ x_1 \\ x_0 \\ x_{-1} \e... ...ay}{l} x_{n+2} \\ x_{n+1} \\ x_n \\ x_{n-1} \end{array}\right]$$

Es importante hacer notar que el índice de la matriz de transferencia se refiere al número de veces en que la matriz o matrices de transferencia son multiplicados, es decir, para el caso de una cadena homogénea, como la que estamos tratando, todas las matrices son iguales en cuyo caso se puede hablar del índice como un exponente, pero si nuestra matriz no es homogénea, es decir, por ejemplo que una de sus partículas sea distinta a las demás, o un resorte sea distinto, entonces la matriz de transferencia correspondiente al bloque de cuatro partículas será distinta a las demás, en cuyo caso no se puede tratar el índice de la matriz de transferencia como exponente, también es importante mencionar que en esta formulación matemática trataremos únicamente con cadenas homogéneas; las cadenas no-homogéneas serán tratadas posteriormente, como se había mencionado con anterioridad y en esos casos trataremos las formas particulares de las matrices de transferencia.

Analizando estos dos vectores, vemos que necesariamente tenemos que suponer dos partículas ficticias en cada extremo de la cadena, ya que estamos suponiendo que las partículas, inicial y final interaccionan a segundos vecinos; por lo tanto con esto podemos justificar la suposición de las condiciones a la frontera introducidas con anterioridad.

Podemos ver algunas propiedades, que resultan de la relación $Z_n = T^n Z_0$ en primer lugar esa ecuación se obtuvo suponiendo, un segmento de cuatro partículas sucesivas distinto de cero; pero ahora supongamos que cuatro partículas adyacentes son cero y reescribamos la ecuación de recurrencia (2.14) en la forma siguiente:

$$T^{-n} \left[\begin{array}{l} 0 \\ 0 \\ x_n \\ x_{n-1} \end{... ...\left[\begin{array}{l} x_2 \\ x_1 \\ 0 \\ 0 \end{array}\right]$$

En donde hemos introducido las condiciones a la frontera y el hecho de que $\vert T\vert\neq 0$. Si para que se cumpla nuestra hipótesis, suponemos que $x_1$ y $x_2$ son cero, entonces como $T^{-n}\neq 0$, esto implica que:

$$\left[\begin{array}{l} 0 \\ 0 \\ x_n \\ x_{n-1} \end{array}\right] = 0$$

y por lo tanto que $x_n =0$, lo cual quiere decir que todas las componentes del vector son cero y como el eigenvector cero no lo consideramos como eigenvector, podemos concluir que es imposible que el bloque formado por cuatro partículas adyacentes sea cero, sin que el desplazamiento de cada una sea cero; para nuestro caso podemos suponer que $x_1$ y $x_2$ son distintas de cero, ya que si ambos fueran cero obtendríamos un vector con componentes cero, debido a que $x_0$ y $x_{-1}$ son cero por las condiciones suplementarias.