Ahora regresemos a nuestro mapeo conjugado canónico.
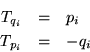
Si recordamos que ![]() es una base de
es una base de ![]() y los funcionales
y los funcionales
![]() una base de
una base de
![]() entonces podemos
encontrar una matriz que nos representa a esta función. Esta matriz es
entonces podemos
encontrar una matriz que nos representa a esta función. Esta matriz es ![]()
![\begin{eqnarray*}
J & = &
\left[ \begin{array}{cccccc\vert cccccc}
& & & & & &...
...1 & & & & & & & \\
& & & & & 1 & & & & & &
\end{array}\right]
\end{eqnarray*}](img355.gif)
Así
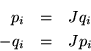
Ahora lo que nos interesa es extender este mapeo a todo el espacio.
Esto lo hacemos por medio de la siguiente definición:
Cabe hacer notar que el caso en que nuestro campo de escalares sea real,
entonces la matriz ![]() seguirá representando a nuestra transformación. En el
caso complejo no sucede así, ya que el mapeo conjugado canónico no es un
mapeo lineal, por aparecer un conjugado complejo.
seguirá representando a nuestra transformación. En el
caso complejo no sucede así, ya que el mapeo conjugado canónico no es un
mapeo lineal, por aparecer un conjugado complejo.
Sin embargo, en cualquiera de estos dos campos es posible ver que
Remarcando que ![]() ,
, ![]() pertenecen a
pertenecen a ![]() entonces
entonces ![]() es un
elemento de nuestro campo de escalares, cosa que puede no suceder si
tenemos otro espacio vectorial.
es un
elemento de nuestro campo de escalares, cosa que puede no suceder si
tenemos otro espacio vectorial.
Así hemos encontrado una matriz tal que en ![]() el paréntesis de
Poisson puede ser sustituido por un producto interno.
el paréntesis de
Poisson puede ser sustituido por un producto interno.