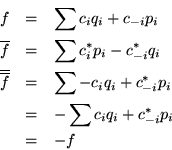


Next: Construcción de una nueva
Up: Los paréntesis de Poisson
Previous: Extensión de la definición
Contents
Nos preguntamos si podemos definir un producto interno como los
paréntesis de Poisson directamente, es decir si
cumple con los axiomas:
La contestación es no, porque
Pero si ahora definimos la funcional lineal 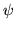 de la manera:
de la manera:
tendremos que 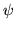 es un producto interno. La verificación de esto es
muy fácil, tan solo por aplicar varias veces las propiedades de los
paréntesis de Poisson a
es un producto interno. La verificación de esto es
muy fácil, tan solo por aplicar varias veces las propiedades de los
paréntesis de Poisson a
y recordando que
Algo muy conveniente es averiguar la relación que guardan los productos
internos, hasta ahora definidos, los cuales han sido denotados por 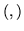 y por
y por 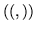 .
.
Pero antes veamos el siguiente lema
Lema 1.-
tomemos
entonces x, como eneada está representada por
Pero esto es lo mismo que buscar una matriz tal que a la mitad
inferior de
lo suba cambiándole el signo y a la parte superior simplemente la baje,
pero esto hace una matriz de la forma
que es precisamente 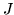 multiplicando a
multiplicando a  , por lo tanto
, por lo tanto
Corolario.- Si M es una transformación lineal, entonces
por el lema 1, entonces
Regresemos a los productos internos
pero
por lo tanto
pero
Así
y como 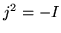 .
.
en resumen
La operación de conjugar canónicamente, es una operación semi-involutoria
ya que si
Así



Next: Construcción de una nueva
Up: Los paréntesis de Poisson
Previous: Extensión de la definición
Contents
Pedro Hernandez
2004-01-14
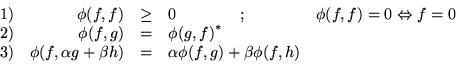
![]() de la manera:
de la manera:
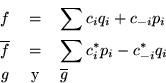
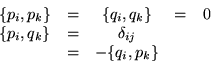
![\begin{displaymath}x =
\left[\begin{array}{c} C_1\\ C_2 \\ \vdots \\ C_n \\
C_{-1} \\ C_{-2}\\ \vdots \\ C_{-n}
\end{array}\right]\end{displaymath}](img372.gif)
![\begin{displaymath}\overline{x} =
\left[\begin{array}{c}
-C_{-1}^* \\ -C_{-2}^...
...}^* \\
C_1^* \\ c_2^* \\ \vdots\\ C_n^*
\end{array}\right]
\end{displaymath}](img374.gif)
![\begin{displaymath}
\left[\begin{array}{c} C_1^* \\ C_2^* \\ \vdots \\ C_n^* \\
C_{-1}^* \\ C_{-2}^* \\ \vdots \\ C_{-n}^*
\end{array}\right]\end{displaymath}](img375.gif)
![\begin{displaymath}\left[ \begin{array}{cccccc\vert cccccc}
& & & & & & -1 & &...
...& & & & & & & \\
& & & & & 1 & & & & & &
\end{array} \right]\end{displaymath}](img376.gif)