La teoría de las álgebras de Lie clasifica las mismas, en terminos de los posibles diagramas de raíces que puedan existir, y también demuestra que los vectores raíz pueden tomar sólo ciertos valores racionales y que para los ángulos entre los vectores, también sólo son permitidos algunos valores. Sin embargo, a nosotros sólo nos interesan las posibles aplicaciones de esta teoría a la mecánica hamiltoniana, y nuestro interés se debe en parte a que esta teoría nos permite, algunas veces, construir sistemas de coordenadas canónicas.
En este trabajo nos es imposible, debido a la brevedad del espacio con el que contamos, desarrollar formalmente los hechos necesarios para demostrar nuestras afirmaciones, así que sólo mencionaremos las referencias, las cuales son: Jacobson [2] y el libro de Rowlatt [21]
Si uno acepta la teoría, es posible entender algunos ejemplos que daremos a continuación.
Tomemos a ![]() operando sobre
operando sobre ![]()
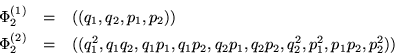
La tabla de conmutación es:
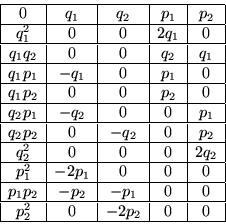
Una subálgebra de Cartan es la generada por los elementos ``diagonales".
los vectores raíz son por tanto
su diagrama de raíces es.
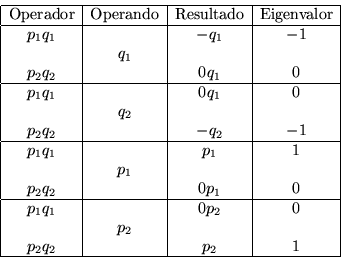
Ahora tomemos a ![]() operando sobre
operando sobre ![]()
los eigenvalores y eigenvectores son:
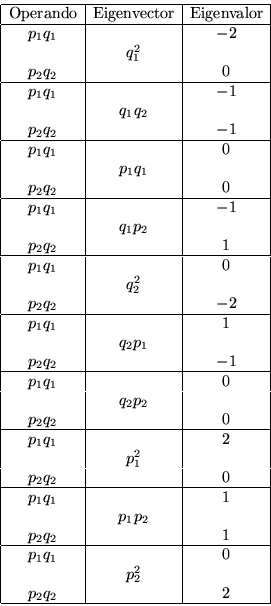
Los vectores son por tanto
![\begin{displaymath}\begin{picture}(110,110)(10,20)
\put(50,60){\vector(0,1){40}...
...$ + $}}\\
\put(46,80){\shortstack[r]{$ - $}}\\
\end{picture}\end{displaymath}](img985.gif)
Con un poco de reflexión, o bien usando la teoría completamente elaborada,
uno encuentra ciertos vectores (![]() ,
,![]() en estos casos), en términos de los cuales
los vectores de peso se escriben simplemente como sumas y diferencias, las
cuales podemos usar como etiquetas para los vectores del espacio de los diagramás.
en estos casos), en términos de los cuales
los vectores de peso se escriben simplemente como sumas y diferencias, las
cuales podemos usar como etiquetas para los vectores del espacio de los diagramás.
Si definimos un mapeo de ![]() en el espacio de vectores de peso de la
siguiente manera:
en el espacio de vectores de peso de la
siguiente manera:
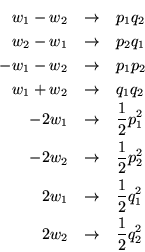
Ahora definimos
En general para ![]() , los generadores del álgebra de Lie quedan escritos
de la siguiente manera:
, los generadores del álgebra de Lie quedan escritos
de la siguiente manera:
Los elementos ![]() son los generadores de la subálgebra de Cartan.
son los generadores de la subálgebra de Cartan.
Estas definiciones establecen que ![]() es una álgebra de Lie simple
es una álgebra de Lie simple ![]() de matrices simplécticas:
de matrices simplécticas:
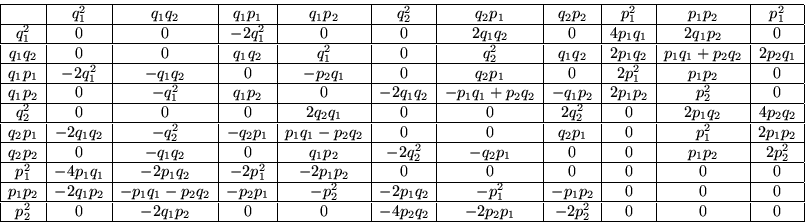
Para el caso de ![]() se obtienen los siguientes diagramas de peso
se obtienen los siguientes diagramas de peso
![\begin{displaymath}\begin{picture}(100,110)(10,20)
\put(00,70){\vector(0,1){20}...
...
\put(100,30){\shortstack[r]{$\phi_3^{(1)}$}}\\
\end{picture}\end{displaymath}](img999.gif)
Estas son las raíces, que no pueden ser escritas como la suma de otras raíces. Sus eigenfunciónes asociadas son entonces, un conjunto degenerado para el ágebra de Lie. En este sentido de todos los demás elementos pueden ser reducidos a partir de las raíces primitivas por medio de conmutadores y combinaciones lineales.
Otros hechos de interés para la mecánica hamiltoniana son las raíces de máximo peso, estas serán las raíces que yacen sobre las caras exteriores del octaedro, que define el diagrama de raíces. La suma de estas raíces, no son
raíces a su vez y por tanto sus eigenfunciones asociadas conmutan. Un ejemplo de esto último, es el conjunto formado por
Las reglas de conmutación son:
![\begin{eqnarray*}
\mbox{$[ p_iq_i,p_jq_j] $} & = & 0\\
\mbox{$ [p_iq_i,\frac{...
... $} & = & \delta_{ij}q_i^2\\
\mbox{$ [q_i^2,q_j^2] $} & = & 0
\end{eqnarray*}](img1001.gif)
si
![\begin{eqnarray*}
\mbox{$ [f,g]$} & = & \lambda g\\
\mbox{$ [f,\frac{\mbox{ln } g}{\lambda} ] $}& = & 1
\end{eqnarray*}](img1002.gif)
Un esquema similar fué usado por McIntosh y Dulock [5] para construir coordenadas canónicas relacionadas con la degeneración accidental de oscilador armónico. A este respecto podemos decir que el conjunto
![]() no solamente forma un álgebra de Lie, sino además contiene
varias subálgebras de interés. Por ejemplo, tomando en cuenta la
identidad de Jacobi, todos los elementos que conmutan con un elemento fijo
forman una subálgebra. Una subálgebra de este tipo tiene interés en
conección con el oscilador armónico, por que el hamiltoniano de este es
un elemento de
no solamente forma un álgebra de Lie, sino además contiene
varias subálgebras de interés. Por ejemplo, tomando en cuenta la
identidad de Jacobi, todos los elementos que conmutan con un elemento fijo
forman una subálgebra. Una subálgebra de este tipo tiene interés en
conección con el oscilador armónico, por que el hamiltoniano de este es
un elemento de ![]() y consecuentemente los elementos que conmutan
con él son constantes de movimiento para el oscilador armónico, y ellos
forman un álgebra de Lie isomorfa a
y consecuentemente los elementos que conmutan
con él son constantes de movimiento para el oscilador armónico, y ellos
forman un álgebra de Lie isomorfa a ![]() .
.