Algunos resultados y consideraciones

Trataremos de ver que forma necesitan tener los elementos $g$ para que conmuten con un elemento fijo $f$, el cual es normal.

Como $f$ es normal, tiene un sistema de eigenvectores $g_i = \Psi_n^{(i)}$, para los cuales

$$[f,g_i]= \lambda_i g_i$$

$g$ puede ser expandido en términos de los $g_i$

$$g=\sum_{ij\ldots n}a_{i,j\ldots n}g^{\alpha_i}_1 g^{\alpha_j}... ...a^{'}_i}_{-1} g^{\alpha^{'}_j}_{-2}\ldots g^{\alpha^{'}_m}_{-m}$$

Por tanto

$$\begin{eqnarray*}[f,g]& = &\sum a_{i,j,\ldots, n} [f,g_1^{\alpha_i} g_2^{\alpha_... ...{'}_n)\lambda_m) g_1^{\alpha_i},\ldots , g_{-m}^{\alpha^{'}_n} \end{eqnarray*}$$

Si queremos que $[f,g]\ =\ 0$ entonces

$$a_{ij..n}((\alpha_i-\alpha^{'}_i)\lambda_1+(\alpha_j-\alpha^{'}_j)\lambda_2 +\cdots +(\alpha_n-\alpha^{'}_n)\lambda_m) = 0$$

Para que este producto sea cero, o los coeficientes $a_{i,j...n}$ son cero, o lo son los otros factores.

En el caso en que $(\alpha_i-\alpha^{'}_i)\lambda_1+\cdots+ (\alpha_n-\alpha^{'}_n)\lambda_m \neq 0$ el coeficiente correspondiente,

$$a_{ij..n} = 0$$

Por tanto

$$g=\sum_{{\bf\alpha\cdot\lambda}= 0} a_{ij...n}g_1^{\alpha_i... ...g_m^{\alpha_n}g_{-1}^{\alpha^{'}_i}\ldots g_{-m}^{\alpha^{'}_n}$$

donde

$$\begin{eqnarray*} {\bf\alpha } & = & (\alpha_i,\alpha_j,\ldots \alpha_n,\alpha^{'}_i,\ldots, \alpha^{'}_n) \end{eqnarray*}$$

y

$$\begin{eqnarray*} {\bf\lambda } & = & (\lambda_1,\lambda_2,\ldots,\lambda_m, -\lambda_1,\ldots, -\lambda_m) \end{eqnarray*}$$

Si $\lambda_1,\lambda_2,\cdots,\lambda_m$ son mutuamente inconmensurables

$${\bf\alpha \cdot \lambda }= 0$$

sólo puede ser satisfecho si

$$\alpha_r = \alpha^{'}_r$$

de donde g será un polinomio en los monomios de segundo grado $g_{-i}g_i$

$$g=\sum a_{ij...n}{(g_{-1}g_1)}^{\alpha_i} {(g_{-2}g_2)}^{\alpha_j},\ldots, {(g_{-m}g_m)}^{\alpha_n}$$

Por otro lado si los $\lambda^{'}_s$ son conmensurables, otro tipo de polinomios conmutan con f, y no hay mucho que decir.

Hemos visto en el primer capítulo que una transformación canónica, $T$, cumple con

$$[T(x_i),T(x_j)]= [x_i,x_j]$$

En el caso en que

$$[T(x_i),T(x_j)]= -[x_i,x_j]$$

diremos que $T$ es anticanónica.

Hay tres transformaciones, las cuales tienen una gran importancia en la mecánica, y caen en alguna de las categorías acabadas de mencionar. Estas transformaciones se definen relativas a una base fija.

i) El mapeo dual, $M$

$$\begin{eqnarray*} M(f_i) & = & f_{-i}\\ & & \hspace{.6in}i \ > \ 0\\ M(f_{-i}) & = & -f_i \end{eqnarray*}$$

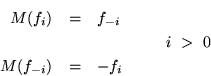
ii) El intercambio de coordenadas y momenta, $X$

$$X(f_i) = f_{-i}$$

iii) El mapeo, inversión del tiempo, $R$

$$\begin{eqnarray*} R(f_i) & = & f_i\\ & & \qquad \qquad i \ > \ 0 \\ R(f_{-i}) & = & -f_{-i} \end{eqnarray*}$$

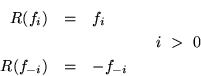
La primera de estas tranformaciones satisface la ecuación

$$\left\{M(f_i),M(f_j)\right\} = \left\{f_i,f_j\right\}$$

y de aquí que sea una transformación canónica.

Las otras dos transformaciones cumplen con:

$$\begin{eqnarray*} \left\{X(f_i),X(f_j)\right\} & = & -\left\{f_i,f_j\right\}\\ \left\{R(f_i),R(f_j)\right\} & = & -\left\{f_i,f_j\right\} \end{eqnarray*}$$

y por tanto son mapeos anticanónicos.

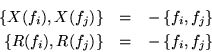
Para definir estos mapeos para cualquier elemento sólo hay que extrapolarlos linelamente.

Algo que podemos hacer con estas transformaciones es representarlas por operadores de la forma $T_f(u) = (\lambda(u) \left\{f,u\right\})$ y expanderlos en términos de sus eigenfunciones.

Se puede verificar que las expresiones cuadráticas correspondientes son:

$$\begin{eqnarray*} m & = & -\sum_{i=1}^n\frac{f_if_i+f_{-i}f_{-i}}{2\left\{f_{-i... ...= & -\sum_{i=1}^n\frac{f_{-i} f_i}{\left\{ f_{-i}, f_i\right\} } \end{eqnarray*}$$

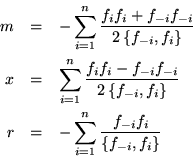
Así que

$$\begin{eqnarray*} M(u) & = & (\lambda(u)\left\{m,u\right\})\\ X(u) & = & (\la... ...eft\{x,u\right\})\\ R(u) & = & (\lambda(u)\left\{r,u\right\}) \end{eqnarray*}$$

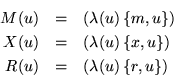
Los paréntesis de Poisson que ocurren en los denominadores son para normalización.

Podemos calcular la composición de estos operadores, por ejemplo:

$$X(R(f_k))=\left\{\begin{array}{cc} f_{-k}, & k>0\\ -f_{-k}, & k<0 \end{array} \right.$$

$$= M(f_k)$$

Las combinaciones posibles están en la siguiente tabla.

$$\begin{tabular}{\vert c\vert ccc\vert} \hline & M & X & R \\... ...\ X & R & I & M \\ R & -X & -M & I \\ \hline \end{tabular}$$

donde I es el mapeo identidad.

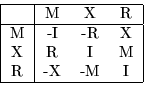
El mapeo identidad I, no puede ser escrito como un operador por medio de los paréntesis de Poisson. Sin embargo los otros tres operadores tienen la siguiente tabla de paréntesis de Poisson.

$$\left\{X,R\right\}= 2M$$

$$\left\{M,R\right\}= 2X$$

$$\left\{X,M\right\}= 2R$$

Así vemos que estos operadores se comportan como si fueran un conjunto de cuaterniones.

Si tomamos un operador normal arbitrario $h\in\phi^{(2)}$ el cual, tiene una expansión, en términos de sus eigenfunciones,

$$h=\sum\frac{\lambda_i f_{-i} f_i }{ \left\{f_{-i},f_i\right\} }$$

y se aplican los tres operadores $X$, $M$, $R$, definidos con respecto a la base de sus eigenfunciones, tenemos

$$T_h(T_r(u)) = T_r(T_h(u))$$

mientras que

$$\begin{array}{ccc} T_h(T_x(u)) & = & -T_x(T_h(u))\\ T_h(T_m(u)) & = & -T_m(T_h(u)) \end{array}$$

de tal manera que en el sentido matricial $h$ y $r$ conmutan, mientras que $h$ y $x$ al igual que $h$ y $m$ anticonmutan. La existencia de estos dos últimos operadores debería haber sido suficiente para asegurar que los eigenvalores ocurren en parejas negativas.

Es bueno hacer notar que los mapeos lineales definidos en $\phi^{(1)}$ pueden ser extendidos a $\phi^{(k)}$, en la misma manera que se definió canónico conjugado. Por ejemplo el mapeo $M$ puede ser definido sobre $\phi^{(2)}$ de la siguiente manera:

$$M(f_if_j) = M(f_i)M(f_j)$$

y cumple con

$$\left\{M(f_if_j),M(f_kf_l)\right\} =-\left\{f_if_j,f_kf_l\right\}$$

Mientras que $X$ satisface

$$\left\{X(f_if_j),X(f_kf_l)\right\}=\left\{f_if_j,f_kf_l\right\}$$

Uno de los posibles temas relacionados, con estos resultados, es la extensión de la definición de mapeo canónico a espacios $\phi_n^{(k)}$. Cosa que parece ser llevada a cabo con algún sentido si se sigue la idea de $\phi_n^{(1)}$ y el concepto de producto interno en $\phi^{(k)}$.

Análogamente, el concepto de automorfismo es un concepto con interés, y debido a que ciertos tipos de transformaciones en las álgebras de Lie simples sólo son cambios de base, sería interesante averiguar si nuestro $\phi^{(2)}$es simple.

Un hecho muy importante, al que no hemos dedicado tiempo es el concepto de álgebra conmutativa con un elemento fijo.

Su importancia radica en el hecho de que esta puede ser representada por el grupo de simetrías $SU(n)$, [17,18,19].

Otro resultado que hemos pasado por alto es la representación del grupo simpléctico, $S_{p_n}$, por $\phi^{(2)}$