


Next: Bibliograf´ia
Up: INSTITUTO POLITECNICO NACIONAL Escuela
Previous: Geometrías Simpléctica y Ortogonal
Contents
Tomemos el álgebra de Lie formada por 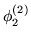 .
.
Consideremos el subespacio
pero una subálgebra de Cartan es
de aquí vemos que el concepto de conjunto maximal de operadores que conmutan
entre si no coincide con el de subálgebra de Cartan.
Es bueno hacer ver que 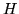 no es una subálgebra de Cartan. Para esto,
supongamos que sí lo fuera, entonces el conmutador del elemento del álgebra
de Lie
no es una subálgebra de Cartan. Para esto,
supongamos que sí lo fuera, entonces el conmutador del elemento del álgebra
de Lie
con el elemento de 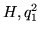 nos debe dar nuevamente un elemento de
nos debe dar nuevamente un elemento de 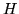 , es
decir, una combinación lineal de
, es
decir, una combinación lineal de 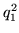 ,
, 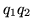 y
y 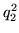 .
.
y este elemento claramente no pertenece a 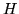 .
.
Pedro Hernandez
2004-01-14
![]() .
.
![\begin{displaymath}\begin{array}{rl}
H \; = & (( q_1^2,q_1q_2,q_2^2))\\
\mbox...
...$} \; = & 0 \\
\mbox{$[ q_1q_2,q_2^2]$} \; = & 0
\end{array}\end{displaymath}](img1103.gif)
![]() .
.