Geometrías Simpléctica y Ortogonal

El objetivo de este apéndice es listar los principales resultados de la geometría simpléctica, y hacer algunas comparaciones con los análogos de la geometría ortogonal. En ningun momento se ha tratado de demostrar algunas de las afirmaciones, ya que este material se encuentra claramente expuesto, en su totalidad, en el libro de Artin [1].

Sea $V$ un espacio vectorial, tanto por la izquierda como por la derecha, de dimensión $n$ sobre un campo $K$, tal que

$$\begin{array}{ccc} a {\bf x} = {\bf x} a;& a\in K,& {\bf x} \in V \end{array}$$

Supongamos que se tiene definida una función de $V \times V$ en $K$, denotada por $XY$ tal que cumpla con las siguientes reglas:

$$\begin{array}{rclc} (X_1 +X_2)Y & = & X_1Y + X_2Y & \\ X(Y... ... = & a(XY) & \qquad (A.1)\\ X(aY) & = & a(XY) & \end{array}$$

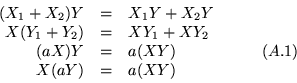
Pensaremos intuitivamente, que $X^2$ $=X$ $X$ es algo que así como ``la longitud" del vector $X$, y de $XY$ pensaremos que es el ``el ángulo'' entre $X$ y $Y$.

Diremos que un producto de este estilo define una ``estructura métrica" sobre $V$ e investigaremos primero, como una estructura de este tipo puede ser descrita por una base $A_I,A_2,\cdots,A_n$ de $V$.

Sean

$$\begin{array}{crll} (A.2) \qquad & A_iA_j = & g_{ij}\in K, ... ...) \qquad & XY = & \sum_{v,u=1}^n g_{vu} X_v Y_u & \end{array}$$

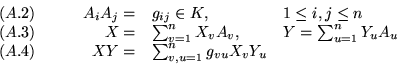
De aquí vemos que si conocemos las constantes $g_{ij}$, entonces conoceremos $X$ $Y$.

Si, reciprocamente, ahora seleccionamos un conjunto de constantes arbitrarias $g_{ij}$ en $K$, y definimos un producto $X$ $Y$, ( de los factores dados por (A.3)), por medio de (A.4), este producto satisface las reglas dadas en (A.1).

Si en (A.4) tomamos $A_i$ por $X$ y $A_j$ por $Y$, obtendremos nuevamente (A.2).

De todo lo anterior vemos que el estudio de las funciones biliniales es equivalente al estudio de las estructuras métricas de $V$.

Dado que las constantes $g_{ij}$ sólo dependen de la selección de la base, ahora veremos como un cambio de ésta, las puede afectar.

Sea $B_I,B_2,\ldots,B_n$ una nueva base de $V$, entonces

$$\mbox{$B_j=\sum_{v=1}^n a_{vj}A_v,\hspace{.2in} a_{ij}\in\kappa$ }$$

Los $B_j$ formarán una base si y solamente si det $(a_{ij})\neq 0$.

Con la nueva base construimos las nuevas constantes $g'_{ij}$

$$\begin{array}{crl} g\prime_{ij}= & B_iB_j = & \sum_{v,u}a_{v... ... a_{ui} A_u\\ & = & \sum_{v,u}a_{vi}g_{vu}a_{uj} \end{array}$$

Lo cual en forma matricial quiere decir:

$$\begin{array}{crl} & (g'_{ij}) = & (a_{ji})(g_{ij})(a_{ij})\... ...uad & (g'_{ij}) = & {(a_{ij})}^T (g_{ij})(a_{ij}) \end{array}$$

Diremos que $A$ es ortogonal a $B$ si $AB=0$.

¿En que estructuras métricas $AB=0$ implica $BA = 0$ ?

La respuesta es que hay dos tipos de estructuras métricas con esta propiedad:

1)

La geometría simpléctica

$$\begin{array}{ccrlc} & i) & X^2 = & 0 & \forall x\in V\\ \Rightarrow & ii) & XY = & -YX & \end{array}$$

(ii) no es equivalente a (i)

como lo muestra el caso especial $Y = X$ con característica de $K$ igual a 2.

Para las constantes $g_{ij}$ obtenemos:

$$\begin{array}{crlc} & g_{ij}= & -g_{ji} \quad , \quad g_{ii}... ... 0 \quad \mbox{si y s\'olo si } & g_{ij} = -g_{ji} \end{array}$$

(A.6) es la condición necesaria y suficiente para una geometría simpléctica y de aquí que una geometría de este tipo es equivalente al estudio de las formas bilineales antisimétricas.

2)

La geometría ortogonal.

$$XY = YX$$

El kernel izquierdo de una funcion $XY$ se define como

$$V_I=\left\{ X\in V \mid XY=0 \mbox{, }\ \forall Y\in V\right\}$$

El kernel derecho es

$$V_D=\left\{ Y\in V\mid XY=0 \mbox{ , }\ \forall X\in V\right\}$$

Con una geometría simpléctica o una ortogonal

$$V_D = V_I$$

De aquí que definamos kernel de $V$ como el radical de $V$, para estas geometrías.

Definición.- Un espacio es llamado isotrópico si todos los productos entre vectores del espacio son cero. Los subespacios 0 y el radical son ejemplos de espacios isotrópicos. Un vector $A$ es isotrópico si $A^2=0$. De aquí que en una geometría simpléctica cada vector es isotrópico.

Definición.- Llamaremos a un espacio vectorial $\: V$, con una estructura métrica, no singular si los kernels de su producto son 0.

El determinante $(g_{ij})=G$ será llamado el discriminante de $V$. La condición necesaria y suficiente para que $V$ sea no-singular es que $G\neq 0$.

Definición.- Un plano no-singular que contenga un vector isotrópico será llamado un plano hiperbólico y este siempre puede ser expandido por una pareja $N$, $M$ de vectores los cuales satisfacen

$$N^2=M^2=0 \quad ,\quad NM=1$$

Para la geometría cotidiana tenemos el siguiente.

Teorema.- Un espacio con geometría ortogonal es una suma ortogonal de líneas

$$V=<A_1>+<A_2>+\cdots +<A_n>$$

Los $A_i$ son llamados una base ortogonal de $V$. $V$ es no-singular si y sólo si ninguno de los $A_i$ es isotrópico.

Y el análogo en la geometría simpléctica es el siguiente.

Teorema.- Un espacio simpléctico no-singular es una suma ortogonal de planos hiperbólicos, en otras palabras es un espacio hiperbólico, su dimensión siempre es par.

Definición.- Un subespacio isotrópico $U$ es llamado isotrópico maximal si $U$ no es un subespacio propio de algun subespacio isotrópico de $V$.

Teorema.- Todos los subespacios isotrópicos maximales de un espacio no-singular $V$ tienen la misma dimensión $r$.

El invariante $r$ de $V$ es llamado el índice de $V$.

Teorema.- La dimensión de un subespacio hiperbólico maximal es $2r$ donde $r$ es el índice de $V$, $\mbox{dim } V = n \; \geq \; 2r$ y el máximo valor para $r,\: \frac{1}{2}n$, se alcanza si y sólo si, $V$ mismo es hiperbólico (Por ejemplo en el caso simpléctico).

Cada espacio simpléctico no-singular es hiperbólico

$$\begin{array}{rrl} V \,= & H_{2r}\; = & P_1\bot P_2 \bot.\ld... ...bot P_r\\ & = & <N_1,M_1,N_2,M_2,\ldots,N_r,M_r> \end{array}$$

donde $P_i=<N_i,M_i>$ es un plano hiperbólico.

Los $N_i,N_j$ satisfacen: $\qquad N_i M_j = M_i M_j = 0 \quad , \quad N_i M_j = \delta_{ij}$

Definición.- Una base $\{ N_i,M_j \}$ del tipo anterior es llamada una base simpléctica de $V$.

El discriminante $G$ de una base simpléctica es 1.

Definición.- El grupo de isometrías de un espacio simpléctico no-singular $V = H_{2r}$ de $\mbox{dim } V = 2 r = n$ es llamado el grupo simpléctico y denotado $S_{p_n} (k)$.

Teorema.- Si $V$ es no-singular y $\sigma$ una isometría de $V$ sobre $V$, entonces $\mbox{det } \sigma \: = \: \pm 1$

Definición.- Si det $\sigma=+1$ entonces $\sigma$ es llamada una rotación; si det $\sigma=-1$, es llamada una reflexión.

Teorema.- Cada elemento de $S_{p_n} (k)$ es una rotación.