Los paréntesis de Poisson son de importancia en la mecánica clásica debido a que en primer lugar pueden ser usados para dar un criterio que nos permita ver si un sistema de coordenadas es canónico y en segundo lugar por que pueden ser usados para definir las transformaciones infinitesimales de contacto. Además si se piensa en ellos como un operador bilineal, sobre los espacios de polinomios homogéneos formados de coordenadas y momenta, se pueden usar para definir un producto interno.
El espacio fase junto con sus operadores lineales adquiere una
estructura muy interesante si se toma en cuenta la relación que hay entre
el producto interno y los paréntesis de Poisson. Esta relación nos lleva a
la definición una operación de conjugación para los espacios de monomios;
a una forma canónica para los operadores, en la cual ellos son expresados
como una suma de productos, a un teorema de parejas el cual dice que los
operadores normales deben tener parejas conjugadas de eigenfunciones y
parejas negativas de eigenvalores, y finalmente a sistemas de coordenadas
canónicas relacionados al álgebra de Lie de los operadores formados
por los polinomios de segundo grado homogéneos.
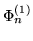y de conjugado canónico
como un álgebra de Lie
