Las ecuaciones de Hamilton en su forma matricial

Las ecuaciones de hamilton son:

$$\dot{p}_i = - \frac{\partial H}{\partial q_i}$$ (1.1)

$$\dot{q}_i = \frac{\partial H}{\partial p_i}$$ (1.2)

lo que haremos será entender bien la forma de estas ecuaciones.

Estas ecuaciones son un caso especial de un sistema expresado por

$$\dot{\xi_i} = \sum_{j} a_{ij} \frac{\partial \Phi(\xi_i)}{\partial \xi_j}$$ (1.3)

donde las $a_{ij}$ pueden ser funciones de las $\xi_i$ y del tiempo y $\xi_i = \xi_i(t)$.

Al sistema de ecuaciones ( 1.3 ) se le llama de Pfaff.

Así las ecuaciones de Hamilton, dentro de un sistema de Pfaff tienen una forma muy simple.

Haciendo

$$\begin{array}{cccc} \xi_i & = & q_i & \\ & & & \mbox{con }i=1,2,\ldots,n \\ \xi_{n+i} & = & p_i & \end{array}$$

tenemos que

$$\left[ \begin{array}{c} \dot{p}_1 \\ \dot{p}_2 \\ \vdots \\ \dot{p}_n \\ \dot{q}_1 \\ \dot{q}_2 \\ \vdots \\ \dot{q}_n \end{array} \right] = \left[ \begin{array}{ccc\vert ccc} . & . & . & -1 & . & . \\ . &... ...partial q_2} \\ \vdots \\ \frac{\partial H}{\partial q_n} \end{array} \right]$$ (1.4)

Vale la pena hablar un poco más acerca de un sistema de Pfaff. Para ello tomaremos las líneas de contorno de $\Phi$ es decir líneas donde $\Phi$ es constante.

Sabemos que el gradiente es un vector dirigido en la dirección de mayor cambio de la función y cuyo tamano queda dado por la derivada de la función en la dirección de mayor cambio.

$$\begin{picture}(200,200)(-20,-20) \put(100,70){\oval(90,90)}\... ...vector(1,0){20}}\\ \put(43,110){\shortstack{IV}} \end{picture}$$

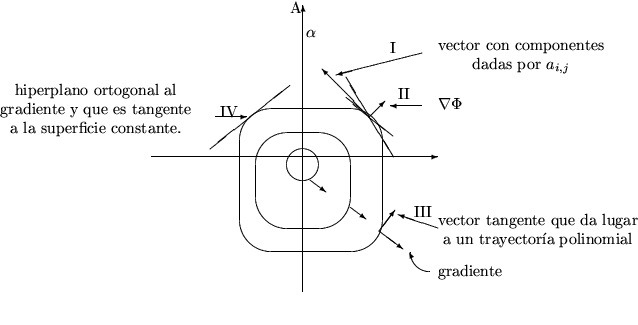
Un corolario es que cualquier hiperplano ortogonal al gradiente (linea IV en el caso de dos dimensiones en la figura) es tangente a la superficie de nivel.

Así, si queremos integrar numéricamente el sistema, lo que tenemos que hacer es tomar el gradiente de $\Phi$ , $\nabla \Phi$, y formar el producto interno con algún vector $\alpha$, el cual puede variar de punto a punto que además puede depender de las $\xi\prime_s$ y posiblemente del tiempo.

Entonces

$$\dot{\xi}_i = (\alpha_i,\nabla\Phi)$$ (1.5)

donde

$$\begin{array}{ccc} \alpha_i & = & \left( \begin{array}{cccc... ...{i2}, & \ldots & ,\alpha_{in} \end{array} \right) \end{array}$$

Hay que hacer notar que tenemos un campo de $\alpha$'s que determinan en cada punto una dirección y también tenemos gradientes de la función $\Phi$ y el producto interior de estos (el de los vectores I y II en la figura) de la velocidad de $\xi$.

Una manera más conveniente de tratar esto es tomar un vector con componentes $\xi_i$ y escribir $\alpha$ como una matriz, operando sobre el vector gradiente.

Lo que quiere decir (1.5) en la figura es que en cualquier punto tendremos un vector gradiente que depende de la función $\Phi$ y una transformación lineal que varía punto a punto y posiblemente con el tiempo, la cual aplicandola al gradiente determina una dirección. Tendremos así un campo de velocidades en cada punto y podemos en cada instante construir un vector, llamado ``vector tangente". Debido a que la solución del movimiento es una curva que tiene una de las líneas III como su tangente en cualquier momento, entonces la línea III es tangente en el sentido en que la dirección con que se mueve la partícula en este momento y cuyo tamaño da la velocidad.

Podemos aplicar algún método numérico, por ejemplo el de Euler o el de Rungge-Kutta, para determinar las trayectorias.

Las ecuaciones de Hamilton las podemos escribir como

$$\begin{array}{ccc} \delta & = & J \partial \end{array}$$

donde $\delta$, representa los vectores tangentes (velocidades), $J$ es la matriz de coeficientes y $\partial$ representa a las componentes del gradiente.

Hemos discutido que esta relación lineal es base de los procesos tanto teórico como numérico, en el sentido, que los vectores tangentes (incremento en las velocidades) cambian con la posición del punto en un intervalo pequeño del tiempo.

Estos incrementos los podemos obtener considerando primero la función H, vemos que su gradiente nos da un vector, que transformamos con la matriz J y esto va a dar un campo de tangentes y la trayectoria que resulta es una trayectoria que siempre tiene estos vectores $\delta$ como vectores tangentes.

En base tanto teórica como numérica se puede desarrollar una serie de potencias, como el método de Euler para resolver un sistema de ecuaciones diferenciales, o si deseamos algo más sofisticado se puede usar el proceso de Rungge-Kutta y efectuar la computación numérica. Esta es una de las grandes ventajas de tener en forma hamiltoniana las ecuaciones de movimiento.

La otra propiedad, que es de gran beneficio, de los sistemas hamiltonianos es que podemos cambiar coordenadas con más facilidad, aunque esto es posible en la formulación de Lagrange. Pero podemos ver más claramente el efecto de este cambio.

Lo primero que haremos será introducir dos conjuntos de coordenadas $\{ p_i, q_i \}$ y $\{ P_i, Q_i\}$ tales que:

$$\begin{array}{ccc} P_i & = & P_i(p_1, p_2, \ldots, p_n, q_1... ...& Q_i(p_1, p_2, \ldots, p_n, q_1, q_2, \ldots, q_n) \end{array}$$

con 1$\leq i \leq$ n.

Del cálculo diferencial sabemos que

$$\begin{eqnarray*} \frac{dP_i}{dt} & = & \sum\left( \frac{\partial P_i}{\partia... ...}{dt}+ \frac{\partial P_i}{\partial q_j} \frac{dq_j}{dt}\right) \end{eqnarray*}$$

con 1 $\leq i \leq$ n.

Para las $Q_i$ tenemos también $n$ ecuaciones de estas. Y estas $2n$ ecuaciones pueden ser escritas en la siguiente forma:

$$\begin{array}{ccc} \left[ \begin{array}{c} \dot{P}_1 \\ \do... ...t{q}_2 \\ \vdots \\ \dot{q}_n \end{array} \right] \end{array}$$

A la matriz que aparece en esta expresión la denotamos por

$$\frac{\partial(P_1,P_2,\ldots ,P_n,Q_1,Q_2,\ldots ,Q_n)} {\partial(p_1,p_2,\ldots ,p_n,q_1,q_2,\ldots ,q_n)}$$

y es la matriz jacobiana de la transformación.

Evitemos por el momento las variables $p'$s y $q'$s y escribamos

$$\begin{array}{cccc} X_i & = & X_i(X^{'}_1,X^{'}_2,\ldots,X^{'}_n), & 1\leq i\leq n \end{array}$$

nuestra relación es:

$$\left[ \begin{array}{c} \dot{X}_1 \\ \dot{X}_2\\ \vdots\\ \dot{X}_n \end{array}\right] = \frac{\partial(X_1,X_2,\ldots,X_n)} {\partial(X^{'}_1,X^{'}_2,\ld... ... \dot{X}^{'}_1 \\ \dot{X}^{'}_2\\ \vdots\\ \dot{X}^{'}_n \end{array} \right]$$ (1.6)

Simbólicamente escribimos

$$\begin{eqnarray*} % latex2html id marker 626\delta & = & \frac{\partial(X_1,X_... ...{'}_2,\ldots,X^{'}_n)} \delta^{'} \qquad (\ref{eq:seis}\mbox{a}) \end{eqnarray*}$$

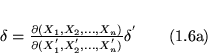
Si suponemos ahora que

$$\begin{array}{cccc} X^{'}_i & = & X_i\left(X_1^{''},X_2^{''... ...X_n^{''}\right) & \mbox{ con } \quad 1\leq i\leq n \end{array}$$

y que

$$\begin{array}{ccc} \left[ \begin{array}{c} \dot{X}_1 \\ \do... ...} \\ \vdots \\ \dot{X}_n^{''} \end{array} \right] \end{array}$$

entonces sustituyendo en la anterior relación tenemos

$$\begin{array}{ccc} \left[ \begin{array}{c} \dot{X}_1 \\ \do... ...} \\ \vdots \\ \dot{X}_n^{''} \end{array} \right] \end{array}$$

y recordando una propiedad de los jacobianos tenemos que:

$$\begin{array}{ccc} \left[ \begin{array}{c} \dot{X}_1 \\ \do... ...} \\ \vdots \\ \dot{X}_n^{''} \end{array} \right] \end{array}$$

Ahora veremos como cambian las derivadas parciales del hamiltoniano

$$H = H (p_1, \ldots, p_n, q_1, \ldots, q_n)$$

cuando cambiamos de sistema de coordenadas.

Por el momento para evitar la distinción entre las coordenadas y los momentos, trabajaremos una función.

$$\Phi = \Phi(x_1,\ldots,x_n)$$

y además con dos sistemas de coordenadas:

$$\begin{array}{cccc} X_i & = & X_i(x^{'}_i,\ldots, x^{'}_n) & 1\leq i \leq n \end{array}$$

Calculemos

$$\frac{\partial\Phi}{\partial x^{'}_i}$$

$$\begin{eqnarray*} \frac{\partial\Phi}{\partial X^{'}_i} & = & \sum_{j=1}^{n}\... ...artial\Phi}{\partial X_j} \frac{\partial X_j}{\partial X^{'}_i} \end{eqnarray*}$$

y tendremos $n$ ecuaciones de este tipo, las cuales pueden ser escritas en la siguiente forma:

$$\left[ \begin{array}{c} \frac{\partial\Phi}{\partial X^{'}_1} \\ ... ...{'}_2} \\ \vdots \\ \frac{\partial\Phi}{\partial X^{'}_n} \end{array} \right] = \left[ \begin{array}{cccc} \frac{\partial X_1}{\partial X^{'}_1} ... ... x_2} \\ \vdots \\ \frac{\partial \Phi}{\partial x_n} \\ \end{array} \right]$$ (1.7)

tenemos así una transformación con casi la misma estructura que la de la transformación de derivadas totales (1.6). Con la diferencia de que en (1.6) fijamos la variable que vamos a derivar y aquí fijamos la variable con respecto a la cual vamos a derivar.

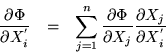
Así vemos que la relación (1.7) casi puede escribirse utilizando una matriz jacobiana y que el casi aparece por las razones expuestas en el párrafo anterior.

Podemos resolver nuestro problema, introduciendo una matriz transpuesta; es decir, si llamamos a la matriz que aparece en (1.7), $M^{-1}$ entonces:

$$\begin{eqnarray*} M^{-1^T} & = & \left[ \begin{array}{cccc} \frac{\partial X_... ...frac{\partial(X_1,\ldots,X_n)}{\partial(X^{'}_1,\ldots,X^{'}_n)} \end{eqnarray*}$$

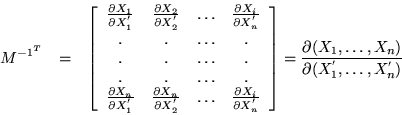
Así tenemos que las ecuaciones (1.7) se escribirán como

$$\begin{eqnarray*} \left[ \begin{array}{c} \frac{\partial \Phi}{\partial X^{'}_1... ...ts \\ \frac{\partial \Phi}{\partial X_n} \end{array} \right] \end{eqnarray*}$$

Simbólicamente lo escribiremos como

$$\partial^{'} = \frac{{\partial(X_1, \ldots, X_n)}^T}{\partial(X^{'}_1,\ldots,X^{'}_n)} \partial$$ (1.8)

Esta ecuación la escribiremos como

$$\begin{array}{ccc} {\left[\frac{\partial(X_1,\ldots,X_n)}{\... ...} \right]}^{T^{-1}} \partial^{'} & = & \partial \end{array}$$

y recordando que para matrices invertibles

$$\begin{array}{ccc} (A^{-1})^T & = & (A^T)^{-1} \end{array}$$

entonces

$$\begin{array}{ccc} \partial & = & {\left[ \frac{\partial(X... ...X^{'}_1,\ldots,X^{'}_n)}\right]}^{-1^T}\partial^{'} \end{array}$$

Utilizando ahora otra relación de los jacobianos que dice

$$\begin{eqnarray*} % latex2html id marker 860 \frac{{\partial(X_1, \ldots, X_n... ...{'}_n)}{\partial(X_1,\ldots,X_n)} \qquad (\ref{eq:ocho}\mbox{a}) \end{eqnarray*}$$

tenemos que

$$\partial = \frac{\partial{(X^{'}_1, \ldots, X^{'}_n)}^T} {\partial(X_1,\ldots,X_n)} \partial^{'}$$ (1.9)

escribiremos nuevamente la ecuación (1.6a) para ver analogías y diferencias con (1.9)

$$\begin{eqnarray*} % latex2html id marker 881 \delta & = & \frac{\partial(X_1, ... ...X^{'}_n)}\delta^{'}\mbox{\hspace{1. in}} (\ref{eq:seis}\mbox{a}) \end{eqnarray*}$$

y vemos que la matriz de transformación es que en una aparece la matriz inversa y transpuesta de la que aparece en la otra.

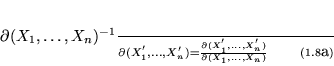
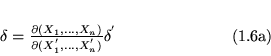
Así que si transformamos $\delta$ podemos transformar inmediatamente $\partial$ y recíprocamente.

Es claro que para hacer esto, es necesario estar trabajando en una región donde la transformación sea invertible, es decir, donde el determinante jacobiano sea distinto de cero.

Regresemos ahora a las ecuaciones hamiltonianas, en las cuales tendremos

$$\begin{array}{ccc} \delta & = & J \partial \end{array}$$

y como

$$\begin{array}{ccc} M^{-1^T} & = & \frac{\partial(X_1, \ldots, X_n)} {\partial(X^{'}_1,\ldots,X^{'}_n)} \end{array}$$

entonces

$$\begin{array}{ccc} M^T & = & \frac{\partial(X^{'}_1, \ldots, X^{'}_n)} {\partial(X_1,\ldots,X_n)} \end{array}$$

por lo tanto

$$\begin{array}{ccc} \delta & = & {M^T}^{-1} \delta^{'} \end{array}$$

y

$$\begin{array}{ccc} \partial & = & M \partial^{'} \end{array}$$

Las ecuaciones de Hamilton las podemos escribir en la forma

$$\begin{array}{ccc} {M^T}^{-1}\delta^{'} & = & J M \partial^{'} \\ \delta^{'} & = & M^T J M \partial^{'} \end{array}$$

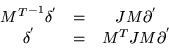
Así vemos que bajo un cambio de coordenadas las ecuaciones hamiltonianas cambian en el hecho de que J será reemplazada por

$$M^T J M$$

donde $M^T$ es la matriz jacobiana de las nuevas coordenadas con respecto a las antiguas.

Así para el sistema hamiltoniano

$$\begin{array}{ccc} M^T & = & \frac{\partial(P_1,P_2,\ldots,... ... {\partial(p_1,p_2,\ldots,p_n,q_1,q_2,\ldots,q_n)} \end{array}$$