


Next: Potencial electrostático
Up: Introducción
Previous: Ecuaciones de movimento
Contents
Se desarrollará ahora la energía cinética de la partícula, tomando en
cuenta la presencia de un potencial vectorial A. Como es bien
sabido, hay que seleccionar A de tal manera que
Donde B es el campo magnético. Además, la función
hamiltoniana toma la forma
Estamos considerando el caso en que el campo de fuerzas producido
por la carga magnética es coulombiano, es decir que
Lo que significa que al integrar el campo sobre una superficie
esférica se tendrá:
Como el segundo miembro es constante, la expresión (I-3-4) indica
que la disminución del campo con la distancia es compensada por el
crecimiento del área.
Nuestro problema consiste ahora en encontrar la forma que debe
tener A para dar lugar a un campo magnético como el que se ha
mencionado. Por el momento vamos a verificar que la función que nos
interesa puede tomarse como
donde  es la carga magnética,
es la carga magnética, 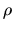 es la posición de la
carga de prueba,
es la posición de la
carga de prueba, 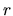 es el radio cilíndrico,
es el radio cilíndrico, 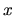 ,
, 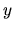 y
y  son las componentes de
son las componentes de 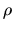 en coordenadas cartesianas.
en coordenadas cartesianas.
Figure 1.2:
coordenadas 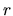 y
y 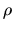
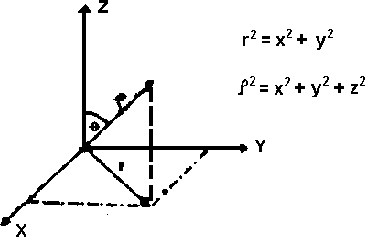 |
Nótese que los coeficientes de 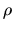 dentro del
paréntesis son adimensionales, teniéndose por consiguiente un
potencial de la forma
dentro del
paréntesis son adimensionales, teniéndose por consiguiente un
potencial de la forma  que es también el caso del potencial
electrostático, y su gradiente es de la forma
que es también el caso del potencial
electrostático, y su gradiente es de la forma 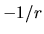 .
Debe observarse también que cuando
.
Debe observarse también que cuando 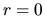 (sobre el eje
(sobre el eje 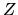 ) el
potencial
) el
potencial 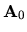 es infinito. Además, cuando
es infinito. Además, cuando 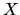 o
o 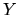 valen cero, se anula dicha función lo que significa que tiene
una dependencia angular, dependencia que por el momento no nos
interesa. Una vez que se tiene
valen cero, se anula dicha función lo que significa que tiene
una dependencia angular, dependencia que por el momento no nos
interesa. Una vez que se tiene 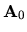 dada por (I-3-5)
encontramos usando (I-3-1) que
dada por (I-3-5)
encontramos usando (I-3-1) que
Como 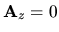 al desarrollar se tiene
al desarrollar se tiene
Para 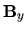 y
y 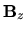 las expresiones son semejantes aunque la
derivación para la componente
las expresiones son semejantes aunque la
derivación para la componente  es algo más complicada, así
es algo más complicada, así
Ese es precisamente el resultado que se buscaba para B. Entonces
da lugar al campo deseado. Es bien sabido que el rotacional de un
gradiente es nulo por lo que nuestro potencial vectorial no está
completamente determinado sino que puede sumársele el gradiente de una
función 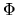 cualquiera, es decir:
cualquiera, es decir:
Dicha operación se conoce como selección de norma, y se sabe
que el potencial vectorial es ambiguo ante una operación de este
tipo, de la misma manera que el potencial escalar es ambiguo ante
el cero de energía potencial; por eso no se afecta un
problema cuando se añade a 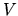 una constante. En el caso del
campo eléctrico, la energía de una partícula con carga
e en su posición actual viene expresada como el trabajo
necesario para llevarla ahí desde una posición de
referencia fijada de antemano; normalmente se fija el cero de
energía en el infinito. Es claro que el cambiar el punto de
referencia, el nuevo valor diferirá del antiguo solo por una
constante; esa es la razón por la que únicamente interesa
conocer diferencias de energía entre dos posiciones. Lo mismo
pasa cuando se tiene un elemento de corriente, solo que por ser
este un vector, debe asignarse a la posición de referencia un
valor y una posición determinados; el momento que tiene un
elemento de corriente en cualquier punto, en presencia de campos
eléctricos y magnéticos es la diferencia de momentos entre las
dos posiciones [2].
En la literatura corrientemente se trabaja con dos normas y aunque
eso no afecta nuestro problema, es importante señalar que en
mecánica cuántica, por ejemplo, hay aspectos que dependen de
la elección de norma. La norma que usamos aquí difiere por
una constante. En el caso del
campo eléctrico, la energía de una partícula con carga
e en su posición actual viene expresada como el trabajo
necesario para llevarla ahí desde una posición de
referencia fijada de antemano; normalmente se fija el cero de
energía en el infinito. Es claro que el cambiar el punto de
referencia, el nuevo valor diferirá del antiguo solo por una
constante; esa es la razón por la que únicamente interesa
conocer diferencias de energía entre dos posiciones. Lo mismo
pasa cuando se tiene un elemento de corriente, solo que por ser
este un vector, debe asignarse a la posición de referencia un
valor y una posición determinados; el momento que tiene un
elemento de corriente en cualquier punto, en presencia de campos
eléctricos y magnéticos es la diferencia de momentos entre las
dos posiciones [2].
En la literatura corrientemente se trabaja con dos normas y aunque
eso no afecta nuestro problema, es importante señalar que en
mecánica cuántica, por ejemplo, hay aspectos que dependen de
la elección de norma. La norma que usamos aquí difiere por
 de la usada tradicionalmente por la literatura
y que en coordenadas polares se escribe como [3]
de la usada tradicionalmente por la literatura
y que en coordenadas polares se escribe como [3]
Esta tiene singularidades en 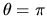 en la dirección negativa
del eje
en la dirección negativa
del eje 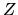 . La otra norma tiene singularidades sólo en la parte
negativa de dicho eje, pero el inconveniente que presenta en nuestros
desarrollos es el hecho de que la separabilidad sí depende de la norma.
El problema que nos ocupa, como hemos dicho, consiste en dos centros
coulombianos separados por una distancia
. La otra norma tiene singularidades sólo en la parte
negativa de dicho eje, pero el inconveniente que presenta en nuestros
desarrollos es el hecho de que la separabilidad sí depende de la norma.
El problema que nos ocupa, como hemos dicho, consiste en dos centros
coulombianos separados por una distancia 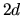 y en ese caso las dos partes
del potencial vectorial son:
y en ese caso las dos partes
del potencial vectorial son:
Entonces el potencial en cualquier punto es la suma de 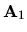 y
y
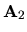 . Al desarrollar la suma se tiene:
. Al desarrollar la suma se tiene:
El hamiltoniano al desarrollarse queda así:
Sin tomar en cuenta el potencial electrostático podemos encontrar
ahora el hamiltoniano en coordenadas elipsoidales. De acuerdo con
(I-3-8). 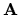 toma la forma:
toma la forma:
El primer término en (I-3-9) ya se calculó en (I-2-4), el segundo se
encuentra fácilmente quedando expresado en coordenadas elipsoidales
como:
Para el tercer término se tiene:



Next: Potencial electrostático
Up: Introducción
Previous: Ecuaciones de movimento
Contents
Pedro Hernandez
2006-02-20
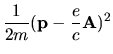
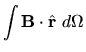

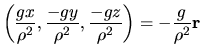
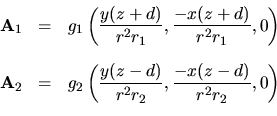
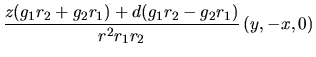
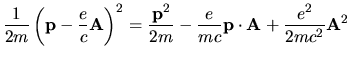
![\begin{eqnarray*}
\frac{e}{c}{\bf p}\cdot{\bf A} & = &
-\frac{p_{\phi}}{d^2}...
..._1-g_2)(1-\eta^2)\xi}{(\xi^2-1)(1-\eta^2)(\xi^2-\eta^2)}\right]
\end{eqnarray*}](img104.png)
![\begin{eqnarray*}
{\bf A}^2 & = & \left[\frac{(g_1+g_2)(\xi^2-1)\eta+
(g_1-g_2)(1-\eta^2)\xi}{(\xi^2-1)(1-\eta^2)(\xi^2-\eta^2)}\right]^2
\end{eqnarray*}](img105.png)