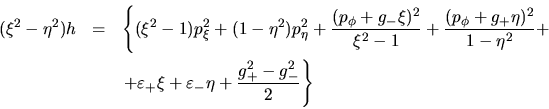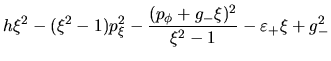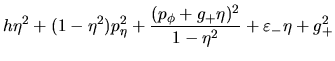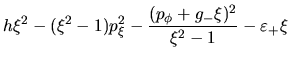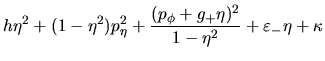Next: Puntos de retorno
Up: Introducción
Previous: Interacción con el campo
Contents
Hasta ahora no hemos tomado en cuenta el efecto de las cargas
eléctricas (si es que hay) de los centros. A estas corresponde un
potencial de la forma.
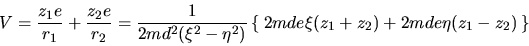 |
(I-4-1) |
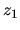 y
y 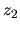 son las cargas eléctricas de los dos centros.
Cuando existe potencial eléctrico el hamiltoniano toma la forma:
son las cargas eléctricas de los dos centros.
Cuando existe potencial eléctrico el hamiltoniano toma la forma:
ya conocemos cada uno de los términos de esa expresión. Tomamos la
convención:
Así logramos simplificar un poco nuestra álgebra. Para
simplificar también los términos de origen electrostático vamos a
definir:
Usando ahora (I-4-3) y (I-4-4), la hamiltoniana quedará como sigue:
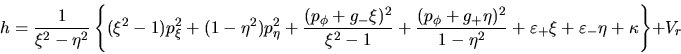 |
(I-4-5) |
Donde 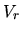 representa a la expresión
representa a la expresión
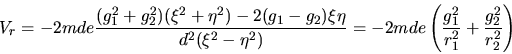 |
(I-4-6) |
La expresión (I-4-5) es la hamiltoniana que usamos en nuestras
ecuaciones de movimiento, siendo dichas ecuaciones de la forma
donde las 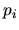 y las
y las 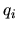 corresponden a las coordenadas y
momentos generalizados. En nuestro caso las ecuaciones (I-4-8)
quedaran así
corresponden a las coordenadas y
momentos generalizados. En nuestro caso las ecuaciones (I-4-8)
quedaran así
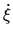 |
 |
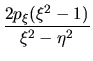 |
(I-4-9) |
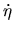 |
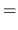 |
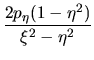 |
(I-4-10) |
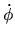 |
 |
 |
(I-4-11) |
 |
 |
![$\displaystyle -\frac{1}{\xi^2-\eta^2}\left\{2\xi\left[
p_{\xi}^2-h-\frac{(p_{\p...
...xi^2-1)^2}\right]
+\frac{2g_-(p_{\phi}+g_-\xi)}{\xi^2-1}
+\varepsilon_+\right\}$](img138.png) |
(I-4-12) |
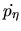 |
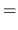 |
![$\displaystyle -\frac{1}{\xi^2-\eta^2}\left\{2\eta\left[
h+p_{\eta}^2-\frac{(p_{...
...eta^2)^2}\right]
-\frac{2g_+(p_{\phi}+g_+\eta)}{\xi^2-1}
-\varepsilon_-\right\}$](img140.png) |
(I-4-13) |
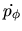 |
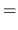 |
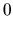 |
(I-4-14) |
Las expresiones
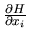 y
y
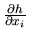 (donde
(donde 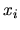 representa coordenadas o momentos)
difieren solamente por el factor
representa coordenadas o momentos)
difieren solamente por el factor 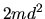 , lo que significa que la
escala de tiempos va a quedar multiplicada por dicha cantidad, por lo
tanto debemos considerar ese factor si queremos ajustar dicha escala de
tiempos.
La expesión (I-4-5) no contiene al tiempo explícitamente, por lo
que
, lo que significa que la
escala de tiempos va a quedar multiplicada por dicha cantidad, por lo
tanto debemos considerar ese factor si queremos ajustar dicha escala de
tiempos.
La expesión (I-4-5) no contiene al tiempo explícitamente, por lo
que 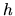 va a ser una constante de movimiento. Además debido a
que la coordenada
va a ser una constante de movimiento. Además debido a
que la coordenada 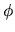 no aparece explícitamente en la
expresión para la hamiltoniana, su momento conjugado
no aparece explícitamente en la
expresión para la hamiltoniana, su momento conjugado  va a ser también constante como se ve en la ecuación (I-4-14).
Que tanto
va a ser también constante como se ve en la ecuación (I-4-14).
Que tanto 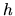 como
como  sean constantes facilita la separación
de variables en el caso de omitir el término
sean constantes facilita la separación
de variables en el caso de omitir el término 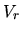 (cuando dicho
término aparece no se puede separar) en la expresión (I-4-5). En
efecto, al multiplicar ambos miembros de (I-4-5) por el factor
(cuando dicho
término aparece no se puede separar) en la expresión (I-4-5). En
efecto, al multiplicar ambos miembros de (I-4-5) por el factor
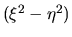 y omitiendo
y omitiendo 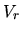 se obtiene
se obtiene
rearreglando términos se tiene
El primer miembro es función sólo de  mientras que el segundo
sólo depende de
mientras que el segundo
sólo depende de  ; la igualdad sólo podrá cumplirse si ambos
miembros son iguales a una constante que llamaremos
; la igualdad sólo podrá cumplirse si ambos
miembros son iguales a una constante que llamaremos 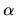 ; en esa
forma hemos logrado obtener dos expresiones separadas:
; en esa
forma hemos logrado obtener dos expresiones separadas:
Una manera alternativa de presentar a (I-4-15) y (I-4-16) es
usando el parámetro 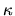 en vez de la cantidad
en vez de la cantidad
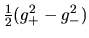 . Así vamos a usarlas también muchas veces. Las
nuevas expresiones van a diferir únicamente en eso y serán.
. Así vamos a usarlas también muchas veces. Las
nuevas expresiones van a diferir únicamente en eso y serán.
Despejando 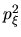 de (I-4-17) se tiene:
de (I-4-17) se tiene:
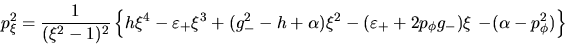 |
(I-4-19) |
Así mismo, despejando 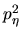 en (I-4-18) obtendremos:
en (I-4-18) obtendremos:
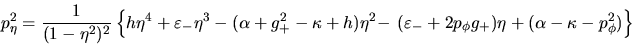 |
(I-4-20) |
Estas dos últimas expresiones serán discutidas con más detalle en
la siguiente sección.
Las ecuaciones (I-4-9) a (I-4-14) pueden tomarse como las componentes de un
vector en seis dimensiones. Dicho vector correspondería a un
gradiente de 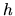 en el espacio fase; este aspecto lo discutiremos más
adelante en la sección correspondiente a la parte numérica del problema.
en el espacio fase; este aspecto lo discutiremos más
adelante en la sección correspondiente a la parte numérica del problema.




Next: Puntos de retorno
Up: Introducción
Previous: Interacción con el campo
Contents
Pedro Hernandez
2006-02-20
![$\displaystyle \frac{1}{2m}\left[{\bf p}-\frac{e}{c}{\bf A}\right]^2+V$](img109.png)
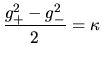
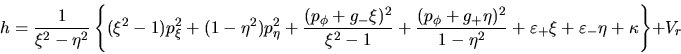
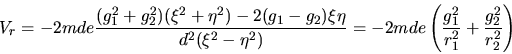
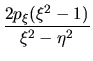
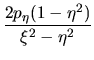
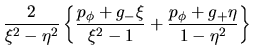
![$\displaystyle -\frac{1}{\xi^2-\eta^2}\left\{2\xi\left[
p_{\xi}^2-h-\frac{(p_{\p...
...xi^2-1)^2}\right]
+\frac{2g_-(p_{\phi}+g_-\xi)}{\xi^2-1}
+\varepsilon_+\right\}$](img138.png)
![$\displaystyle -\frac{1}{\xi^2-\eta^2}\left\{2\eta\left[
h+p_{\eta}^2-\frac{(p_{...
...eta^2)^2}\right]
-\frac{2g_+(p_{\phi}+g_+\eta)}{\xi^2-1}
-\varepsilon_-\right\}$](img140.png)