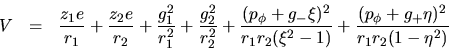Next: Otro método
Up: Introducción
Previous: Potencial electrostático
Contents
Otra cosa que debemos discutir es la determinación de los puntos
clásicos de retorno. Esto lo podemos hacer utilizando las
relaciones (I-4-14). Vemos que hay entonces dos potenciales
efectivos, uno para la variable  y otro para la variable
y otro para la variable
 , y ambos tienen la forma de polinomio de cuarto grado (en
realidad es la raíz de un polinomio de ese grado pero es
más conveniente quitar la raíz cuadrada y el denominador,
porque estos no cambian las raíces de la función).
, y ambos tienen la forma de polinomio de cuarto grado (en
realidad es la raíz de un polinomio de ese grado pero es
más conveniente quitar la raíz cuadrada y el denominador,
porque estos no cambian las raíces de la función).
Figure 1.3:
puntos de retorno
 |
Un potencial de este tipo no es verdadero, sino que pasa algo
semejante a lo que ocurre cuando se usan coordenadas polares para
describir un potencial central de la forma 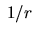 . Con el cambio
a dichas coordenadas aparece además el potencial atractivo, una
parte repulsiva de la forma
. Con el cambio
a dichas coordenadas aparece además el potencial atractivo, una
parte repulsiva de la forma 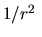 y a la combinación de
esos términos se le conoce como ``potencial efectivo''. El
término adicional es conocido como ``potencial virtual''; la
partícula se mueve bajo la influencia del potencial efectivo
y el radio tendrá un valor mínimo y otro máximo, la
órbita como es sabido, es una elipse con uno de sus focos en el
centro de atracción (en general la curva es una cónica,
dependiendo de la energía de la partícula). El radio
toma valores entre el máximo y el mínimo. Se tiene lo que
se llama una ``barrera centrífuga'' que consiste en que la
partícula no puede acercarse al centro si tiene un momento
angular diferente de cero.
Algo de esa naturaleza ocurre al separar el movimiento en
coordenadas elipsoidales.
y a la combinación de
esos términos se le conoce como ``potencial efectivo''. El
término adicional es conocido como ``potencial virtual''; la
partícula se mueve bajo la influencia del potencial efectivo
y el radio tendrá un valor mínimo y otro máximo, la
órbita como es sabido, es una elipse con uno de sus focos en el
centro de atracción (en general la curva es una cónica,
dependiendo de la energía de la partícula). El radio
toma valores entre el máximo y el mínimo. Se tiene lo que
se llama una ``barrera centrífuga'' que consiste en que la
partícula no puede acercarse al centro si tiene un momento
angular diferente de cero.
Algo de esa naturaleza ocurre al separar el movimiento en
coordenadas elipsoidales.  y
y  tiene potenciales
efectivos que corresponden a curvas de cuarto grado:
tiene potenciales
efectivos que corresponden a curvas de cuarto grado:
puede pensarse que se tiene graficada la energía potencial en
función de  y
y  en la Figura 1.4.
en la Figura 1.4.
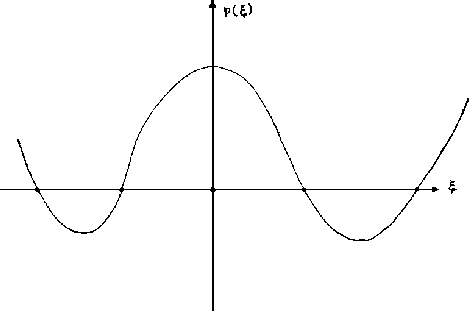
Figure 1.4:
curva de potencial
 |
En la región que hemos sombreado, la energía total es mayor
que la energía potencial, eso quiere decir que la parte
restante puede ser interpretada como la energía cinética.
La dirección del movimiento sólo puede cambiar en los puntos
donde la energía cinética en esta coordenada es nula. Esto
ocurre en los puntos donde la curva intersecta al eje horizontal,
la partícula estará confinada a moverse entre dos elipses
en el caso de  y entre dos hipérbolas para el caso de
y entre dos hipérbolas para el caso de
 .
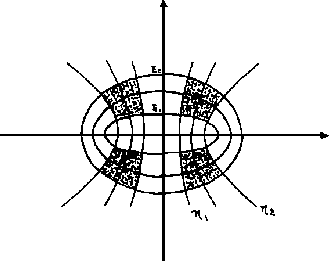
En tres dimensiones el movimiento será posible en la región
comprendida en la intersección de dos elipsoides y dos
hiperboloides de revolución. En la Figura 1.5 mostramos
una sección transversal del caso más general.
.
En tres dimensiones el movimiento será posible en la región
comprendida en la intersección de dos elipsoides y dos
hiperboloides de revolución. En la Figura 1.5 mostramos
una sección transversal del caso más general.
Figure 1.5:
regiones prohibidas
 |
Si nosotros consideramos el potencial producido por las cargas
eléctricas y magnéticas de nuestros centros, se tendrá una
superficie en el espacio de 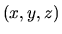 . Si se toman las curvas de
nivel de dicha función entonces tendremos una manera de calcular
la región permitida y la región prohibida del movimiento,
más adelante veremos la manera de hacerlo. El potencial efectivo
va a ser:
. Si se toman las curvas de
nivel de dicha función entonces tendremos una manera de calcular
la región permitida y la región prohibida del movimiento,
más adelante veremos la manera de hacerlo. El potencial efectivo
va a ser:
Podemos considerar muchas posibilidades, por ejemplo, el caso:
que es el problema de un solo centro, aún mas, podemos reducirlo
al problema de Kepler haciendo 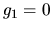 lo que nos daría
secciones cónicas con cierta excentricidad, como es bien sabido.
Veamos lo que ocurrirá en general para dos centros, sin tomar en
cuenta la carga magnética. Si la energía es muy pequeña
en el sentido de ser muy negativa, cuando el movimiento ocurre
cerca de un centro, podemos esperar que la trayectoria de la
partícula sea aproximadamente una elipse alrededor de dicho
centro y fuera de toda influencia del otro. Debido a que dicha
influencia no es nula habrá precesión. En Astronomía este
fenómeno es bien conocido, por ejemplo el movimiento de un
satélite alrededor de un planeta (la Luna alrededor de la
Tierra) dada la influencia del Sol; hay dos centros atractivos
pero el satélite se mueve más cerca del planeta y el
movimiento es casi kepleriano, de no ser por la perturbación
debida al Sol. Lo mismo ocurre con un satélite alrededor de la
Tierra si se considera el efecto por la Luna e ignorando la
influencia del Sol. En toda esta discusión se considera que los
dos centros pemanecen fijos y sólo en éste caso es válido
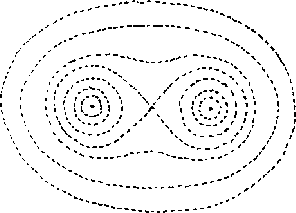
nuestro razonamiento. Para una energía un poco mayor, la
partícula puede girar en torno a los dos centros dando lugar
a varios tipos de trayectorias como se ilustra en la
Figura 1.6. Con energías cada vez mayores pueden
observarse diversas fases de trayectorias hiperbólicas, para las
cuales escapa la partícula.
En las gráficas que se anexan pueden verse diferentes casos.
lo que nos daría
secciones cónicas con cierta excentricidad, como es bien sabido.
Veamos lo que ocurrirá en general para dos centros, sin tomar en
cuenta la carga magnética. Si la energía es muy pequeña
en el sentido de ser muy negativa, cuando el movimiento ocurre
cerca de un centro, podemos esperar que la trayectoria de la
partícula sea aproximadamente una elipse alrededor de dicho
centro y fuera de toda influencia del otro. Debido a que dicha
influencia no es nula habrá precesión. En Astronomía este
fenómeno es bien conocido, por ejemplo el movimiento de un
satélite alrededor de un planeta (la Luna alrededor de la
Tierra) dada la influencia del Sol; hay dos centros atractivos
pero el satélite se mueve más cerca del planeta y el
movimiento es casi kepleriano, de no ser por la perturbación
debida al Sol. Lo mismo ocurre con un satélite alrededor de la
Tierra si se considera el efecto por la Luna e ignorando la
influencia del Sol. En toda esta discusión se considera que los
dos centros pemanecen fijos y sólo en éste caso es válido
nuestro razonamiento. Para una energía un poco mayor, la
partícula puede girar en torno a los dos centros dando lugar
a varios tipos de trayectorias como se ilustra en la
Figura 1.6. Con energías cada vez mayores pueden
observarse diversas fases de trayectorias hiperbólicas, para las
cuales escapa la partícula.
En las gráficas que se anexan pueden verse diferentes casos.
Figure 1.6:
contornos de energía
 |
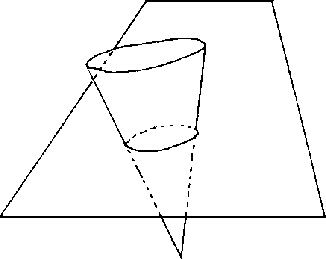
Otro caso que nos interesa es aquel en que hacemos las cargas
eléctricas de un centro iguales a cero, variamos la carga magnética
en el otro. Como dijimos anteriormente, va a ocurrir una precesión de
la trayectoria sobre un cono, en ausencia de potencial repulsivo, pero,
si éste último es incluido para que el movimiento sea separable,
entonces, curiosamente se tiene un plano que interseca al cono dando
una elipse u otra cónica dependiendo de la energía de nuestra
partícula y la única diferencia de este movimiento no contiene
al centro de atracción, ésto se debe a la desviación que se
provoca por la fuerza magnética sobre el movimiento de la
partícula.
Figure 1.7:
cono de Poincaré
 |
Podemos ver otras posibilidades tales como poner cargas
eléctricas y magnéticas juntas, un lado con carga eléctrica
y el otro con carga magnética etc., al final pueden verse
diferentes ejemplos.
Subsections




Next: Otro método
Up: Introducción
Previous: Potencial electrostático
Contents
Pedro Hernandez
2006-02-20