


Next: Potencial repulsivo
Up: Puntos de retorno
Previous: Puntos de retorno
Contents
El tratamiento anterior sobre los puntos clásicos de libración
consiste como hemos visto, en graficar polinomios de cuarto grado
y encontrar sus raíces que corresponden a los puntos
clásicos de retorno. Si se escribe la ecuación separada de
manera un poco diferente podran apreciarse los efectos de variar
ligeramente los diferentes parámetros que intervienen en el
problema.
Reescríbanse las ecuaciones ( I-4-15 ) y ( I-4-16 ) como
sigue:
Para los puntos de libración los momentos se anulan, en ese caso
las ecuaciones (1) quedarán en la forma:
Las expresiones ( 2 ) permiten definir un conjunto de funciones
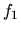 ,
, 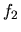 ,
, 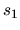 y
y 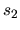 de la manera siguiente:
de la manera siguiente:
Es decir, hay un par de funciones para 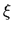 y otro para
y otro para 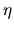 , su
forma es la misma para cada variable con la diferencia de que las
funciones de
, su
forma es la misma para cada variable con la diferencia de que las
funciones de 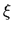 están determinadas por los parámetros:
están determinadas por los parámetros:  ,
,
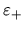 ,
,  ,
, 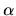 y
y 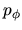 en tanto que las funciones
de
en tanto que las funciones
de 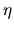 dependen del conjunto:
dependen del conjunto:  ,
, 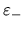 ,
,  ,
, 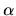 y
y 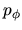 de manera que es suficiente hacer el análisis para las
curvas que se obtienen con una variable y adaptan los resultados del
análisis a las funciones de la otra utilizando sus propios
parámetros haciendo también las consideraciones en que cada
variable tiene sentido físico.
En base a lo anterior vamos a estudiar las curvas para la variable
de manera que es suficiente hacer el análisis para las
curvas que se obtienen con una variable y adaptan los resultados del
análisis a las funciones de la otra utilizando sus propios
parámetros haciendo también las consideraciones en que cada
variable tiene sentido físico.
En base a lo anterior vamos a estudiar las curvas para la variable
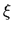 . Hemos quedado en que para los puntos de libración se satisface
la igualdad
. Hemos quedado en que para los puntos de libración se satisface
la igualdad
Es decir, dichos puntos corresponden a las intersecciones de las
curvas dadas por 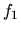 y
y 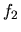 . Analizaremos entonces con algún
detalle dichas funciones.
. Analizaremos entonces con algún
detalle dichas funciones.
Análisis de la Función 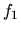 . Esta función
corresponde a una parábola vertical que interseca al eje de las
abscisas en los puntos.
. Esta función
corresponde a una parábola vertical que interseca al eje de las
abscisas en los puntos.
La intersección de la curva con el eje vertical tiene el valor
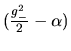 y no depende directamente de
y no depende directamente de  , lo que
indica que si se hace variar la energía en nuestra función
manteniendo fijos los demás parámetros resultará una familia
de parábolas con un punto en común que es precisamente la
intersección con el eje vertical. Debe observarse también que
cuando la energía vale cero la parábola degenera en la
recta:
, lo que
indica que si se hace variar la energía en nuestra función
manteniendo fijos los demás parámetros resultará una familia
de parábolas con un punto en común que es precisamente la
intersección con el eje vertical. Debe observarse también que
cuando la energía vale cero la parábola degenera en la
recta:
con la misma intersección que la familia de
parábolas, siendo también un miembro de dicha familia. La
recta tiene como pendiente el valor
 y de acuerdo
con el signo del parámetro
y de acuerdo
con el signo del parámetro 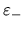 habrá tres
configuraciónes posibles para la familia de parábolas. Eso se
ilustra en las siguientes figuras:
habrá tres
configuraciónes posibles para la familia de parábolas. Eso se
ilustra en las siguientes figuras:
Figure 1.8:
unas curvas
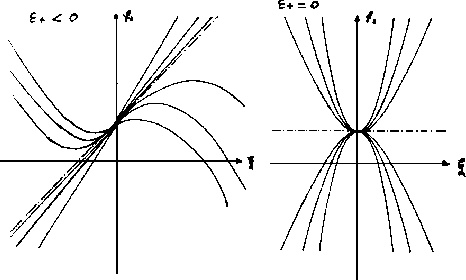 |
Figure 1.9:
más curvas
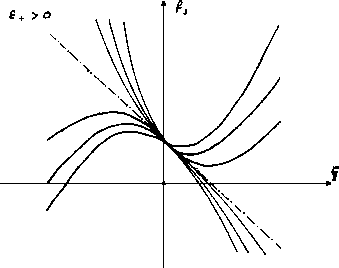 |
Es posible obtener todavía mayor información si escribimos
la primera ecuación de (3) en la siguiente forma.
o bien
La expresion (5) corresponde a la ecuación de una parábola
[22] con vértice en el punto
 y cuyo lado recto es
y cuyo lado recto es 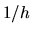 .
Esto permite ver cómo
.
Esto permite ver cómo  influye en la anchura de la curva, por
ejemplo, si
influye en la anchura de la curva, por
ejemplo, si  es muy grande se tendrá una parábola muy aguda
y muy ancha cuando
es muy grande se tendrá una parábola muy aguda
y muy ancha cuando  es pequeña, degenerando en una recta
cuando dicho parámetro se anula. El signo de
es pequeña, degenerando en una recta
cuando dicho parámetro se anula. El signo de  determina si la
curva se extiende hacia arriba o hacia abajo, cuando
determina si la
curva se extiende hacia arriba o hacia abajo, cuando  es
negativa la curva se extiende hacia abajo siendo su vértice un
máximo y para
es
negativa la curva se extiende hacia abajo siendo su vértice un
máximo y para  positiva la curva se extiende hacia arriba
siendo entonces su vértice un mínimo.
El valor del radicando en la expresion (4) determina si la función
cruza o no al eje horizontal. Si dicha cantidad es negativa las
raíces de la ecuación son imaginarias y la curva no tiene
ningún punto en común con el eje. Cuando el radicando es igual
a cero hay una raíz doble que corresponde a tener el
vértice de la curva sobre el eje y cuando el radicando es
positivo la parábola corta al eje en dos puntos.
El parámetro
positiva la curva se extiende hacia arriba
siendo entonces su vértice un mínimo.
El valor del radicando en la expresion (4) determina si la función
cruza o no al eje horizontal. Si dicha cantidad es negativa las
raíces de la ecuación son imaginarias y la curva no tiene
ningún punto en común con el eje. Cuando el radicando es igual
a cero hay una raíz doble que corresponde a tener el
vértice de la curva sobre el eje y cuando el radicando es
positivo la parábola corta al eje en dos puntos.
El parámetro 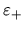 influye en el desplazamiento horizontal
de la curva pero dicho desplazamiento depende también de
influye en el desplazamiento horizontal
de la curva pero dicho desplazamiento depende también de  ,
y como para una configuración de las cargas este último
parámetro puede variar con mayor facilidad podrá decirse que
es el que más influye en el corrimiento lateral del vértice.
Por lo que respecta al movimiento vertical del vértice este
depende de los parámetros
,
y como para una configuración de las cargas este último
parámetro puede variar con mayor facilidad podrá decirse que
es el que más influye en el corrimiento lateral del vértice.
Por lo que respecta al movimiento vertical del vértice este
depende de los parámetros  ,
, 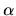 ,
, 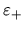 y
y
 , pero
, pero  y
y 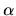 varían con mayor libertad, y variar
estos dos parámetros significa cambiar las condiciones iniciales
del movimiento en tanto que variar
varían con mayor libertad, y variar
estos dos parámetros significa cambiar las condiciones iniciales
del movimiento en tanto que variar 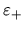 y
y  implica
una alteración de las cargas en los dos centros del sistema que
estamos estudiando.
En la Figura 1.10 mostramos cualitativamente los
diferentes puntos de la curva que pueden tener algún interés.
En otra sección serán presentados varios ejemplos sobre
diferentes posibilidades que tiene el problema donde se
aprovechan las ventajas que tiene el usar computadoras para
realizar todos los cálculos.
implica
una alteración de las cargas en los dos centros del sistema que
estamos estudiando.
En la Figura 1.10 mostramos cualitativamente los
diferentes puntos de la curva que pueden tener algún interés.
En otra sección serán presentados varios ejemplos sobre
diferentes posibilidades que tiene el problema donde se
aprovechan las ventajas que tiene el usar computadoras para
realizar todos los cálculos.
Figure 1.10:
parábola
 |
Analisis de la Función 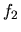 . Se vió ya qué posibilidades
existen para la función
. Se vió ya qué posibilidades
existen para la función 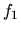 ; enseguida veremos cómo se
comporta
; enseguida veremos cómo se
comporta 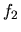 . Lo primero que puede verse es que dicha función
tiene singularidades en los puntos
. Lo primero que puede verse es que dicha función
tiene singularidades en los puntos 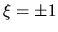 excepto en el caso:
excepto en el caso:
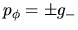 para el que se elimina una de ellas.
Fuera del rango
para el que se elimina una de ellas.
Fuera del rango 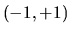 la función no puede ser negativa,
teniendo además como asíntota horizontal a la recta dada por
la función no puede ser negativa,
teniendo además como asíntota horizontal a la recta dada por
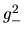 . Dentro de ese rango la función toma valores negativos y su
intersección con el eje vertical tiene el valor
. Dentro de ese rango la función toma valores negativos y su
intersección con el eje vertical tiene el valor 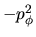 .
Igualando a cero el numerador de la función se encuentra que la
curva toca el eje horizontal en el punto
.
Igualando a cero el numerador de la función se encuentra que la
curva toca el eje horizontal en el punto 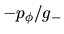 y sólo
en ese punto teniéndose por lo tanto un valor extremo en esa
posición. Hay otro valor extremo en
y sólo
en ese punto teniéndose por lo tanto un valor extremo en esa
posición. Hay otro valor extremo en
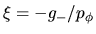 , siendo
entonces recíprocos ambos valores, eso significa que uno de
ellos esta dentro del intervalo
, siendo
entonces recíprocos ambos valores, eso significa que uno de
ellos esta dentro del intervalo 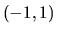 y el otro fuera de él.
Si la curva toca o no al eje dentro de ese intervalo depende de la
relación que haya entre
y el otro fuera de él.
Si la curva toca o no al eje dentro de ese intervalo depende de la
relación que haya entre  y
y  ; además, los dos
puntos mencionados están situados del mismo lado, a la izquierda
si
; además, los dos
puntos mencionados están situados del mismo lado, a la izquierda
si  y
y  tienen el mismo signo y a la derecha si
tienen signo contrario. En caso de que los dos parámetros en
cuestión tengan el mismos valor los puntos extremos coinciden
dando lugar a un punto de inflexion que puede estar en
tienen el mismo signo y a la derecha si
tienen signo contrario. En caso de que los dos parámetros en
cuestión tengan el mismos valor los puntos extremos coinciden
dando lugar a un punto de inflexion que puede estar en 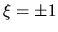 ,
según los signos de
,
según los signos de  y
y  .
La discusión anterior permite que se tenga una idea acerca de los
tipos de curvas que pueden resultar. Eso se ilustra en las
figuras 1.11.
La función no es simétrica en general, lo es sólo en el caso
de que el parámetro
.
La discusión anterior permite que se tenga una idea acerca de los
tipos de curvas que pueden resultar. Eso se ilustra en las
figuras 1.11.
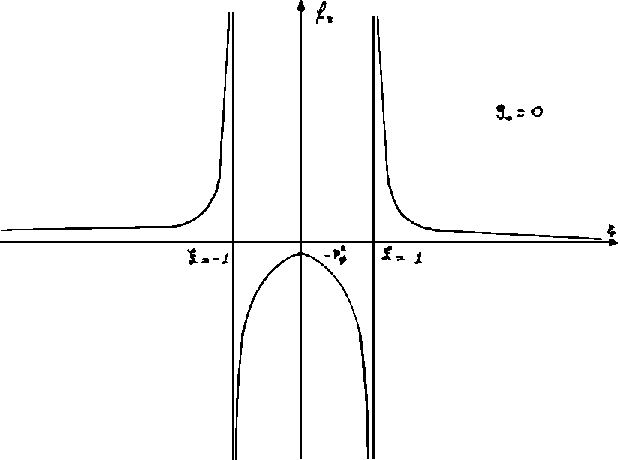
La función no es simétrica en general, lo es sólo en el caso
de que el parámetro  sea nulo y en esas condiciones la
forma de las curvas es como la de la
Figura 1.12.
sea nulo y en esas condiciones la
forma de las curvas es como la de la
Figura 1.12.
Figure 1.11:
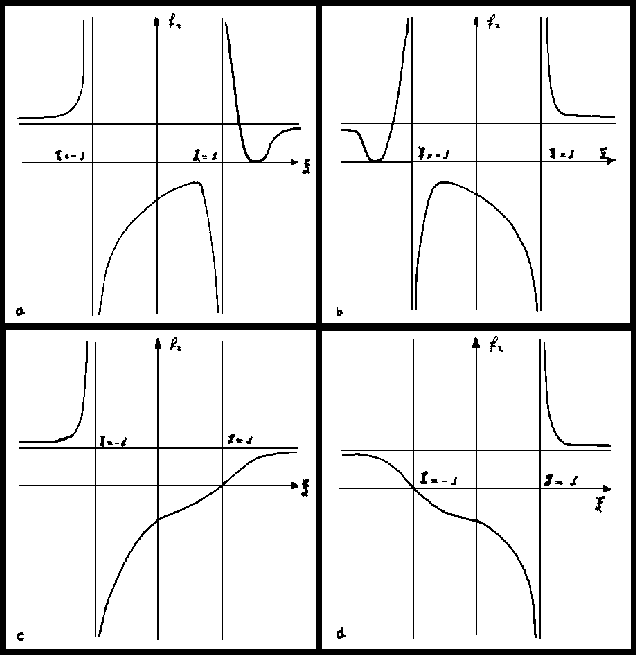 |
Figure 1.12:
 |
Los parámetros  y
y  son los únicos que
caracterizan a la función
son los únicos que
caracterizan a la función 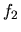 y la manera en que afectan a las
curvas es más fácil de precisar que en el caso de
y la manera en que afectan a las
curvas es más fácil de precisar que en el caso de 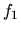 ;
;  determina la posición de la asíntota horizontal y
determina la posición de la asíntota horizontal y
 la intersección de la curva con el eje vertical.
Además, combinados dichos parámetros permiten localizar en
qué posiciones se encuentran los valores extremos. Al variar
nuestros parámetros resultarán familias de curvas, pudiendo
haber transiciones entre los diferentes tipos que hemos mostrado
en las figuras anteriores.
Por lo que respecta a las funciones para la variable
la intersección de la curva con el eje vertical.
Además, combinados dichos parámetros permiten localizar en
qué posiciones se encuentran los valores extremos. Al variar
nuestros parámetros resultarán familias de curvas, pudiendo
haber transiciones entre los diferentes tipos que hemos mostrado
en las figuras anteriores.
Por lo que respecta a las funciones para la variable 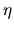 hay
bastante simetría, lo único que debe hacerse es cambiar los
sufijos de las cantidades
hay
bastante simetría, lo único que debe hacerse es cambiar los
sufijos de las cantidades 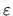 y
y  por el signo
opuesto, fuera de eso, el tratamiento que hay que dar a las curvas
es exactamente el mismo. En el capítulo IV se verán algunos
detalles más sobre estas funciones, para casos especiales y en
el apéndice C hay algunos ejemplos realizados haciendo uso de
una computadora digital; posiblemente algunos detalles sobre las
curvas no sean muy pronunciados en los ejemplos, pero nuestras
figuras fueron construidas así para ilustrar diferentes
posibilidades, además, el tamaño de las hojas de papel en la
computadora no permite graficar rangos muy grandes.
por el signo
opuesto, fuera de eso, el tratamiento que hay que dar a las curvas
es exactamente el mismo. En el capítulo IV se verán algunos
detalles más sobre estas funciones, para casos especiales y en
el apéndice C hay algunos ejemplos realizados haciendo uso de
una computadora digital; posiblemente algunos detalles sobre las
curvas no sean muy pronunciados en los ejemplos, pero nuestras
figuras fueron construidas así para ilustrar diferentes
posibilidades, además, el tamaño de las hojas de papel en la
computadora no permite graficar rangos muy grandes.



Next: Potencial repulsivo
Up: Puntos de retorno
Previous: Puntos de retorno
Contents
Pedro Hernandez
2006-02-20
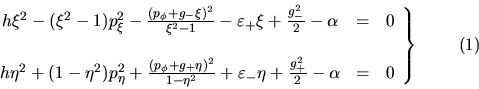
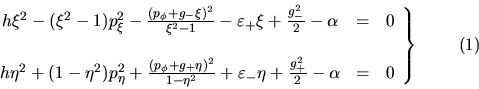
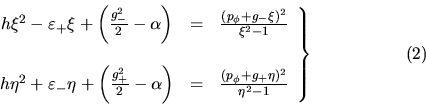
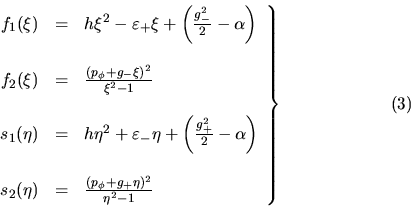
![]() . Esta función
corresponde a una parábola vertical que interseca al eje de las
abscisas en los puntos.
. Esta función
corresponde a una parábola vertical que interseca al eje de las
abscisas en los puntos.
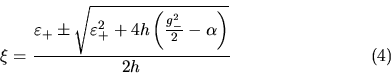
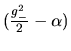 y no depende directamente de
y no depende directamente de 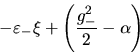
![\begin{displaymath}
\left(\xi+\frac{\varepsilon_+}{2h}\right)^2 = \frac{1}{h}
...
...a-g_-^2+\frac{\varepsilon_+^2}{4h}\right)\right]
\eqno{(5)}
\end{displaymath}](img197.png)
![]() . Se vió ya qué posibilidades
existen para la función
. Se vió ya qué posibilidades
existen para la función ![]() ; enseguida veremos cómo se
comporta
; enseguida veremos cómo se
comporta ![]() . Lo primero que puede verse es que dicha función
tiene singularidades en los puntos
. Lo primero que puede verse es que dicha función
tiene singularidades en los puntos ![]() excepto en el caso:
excepto en el caso:
![]() para el que se elimina una de ellas.
Fuera del rango
para el que se elimina una de ellas.
Fuera del rango ![]() la función no puede ser negativa,
teniendo además como asíntota horizontal a la recta dada por
la función no puede ser negativa,
teniendo además como asíntota horizontal a la recta dada por
![]() . Dentro de ese rango la función toma valores negativos y su
intersección con el eje vertical tiene el valor
. Dentro de ese rango la función toma valores negativos y su
intersección con el eje vertical tiene el valor ![]() .
Igualando a cero el numerador de la función se encuentra que la
curva toca el eje horizontal en el punto
.
Igualando a cero el numerador de la función se encuentra que la
curva toca el eje horizontal en el punto ![]() y sólo
en ese punto teniéndose por lo tanto un valor extremo en esa
posición. Hay otro valor extremo en
y sólo
en ese punto teniéndose por lo tanto un valor extremo en esa
posición. Hay otro valor extremo en
![]() , siendo
entonces recíprocos ambos valores, eso significa que uno de
ellos esta dentro del intervalo
, siendo
entonces recíprocos ambos valores, eso significa que uno de
ellos esta dentro del intervalo ![]() y el otro fuera de él.
Si la curva toca o no al eje dentro de ese intervalo depende de la
relación que haya entre
y el otro fuera de él.
Si la curva toca o no al eje dentro de ese intervalo depende de la
relación que haya entre ![]() y
y ![]() ; además, los dos
puntos mencionados están situados del mismo lado, a la izquierda
si
; además, los dos
puntos mencionados están situados del mismo lado, a la izquierda
si ![]() y
y ![]() tienen el mismo signo y a la derecha si
tienen signo contrario. En caso de que los dos parámetros en
cuestión tengan el mismos valor los puntos extremos coinciden
dando lugar a un punto de inflexion que puede estar en
tienen el mismo signo y a la derecha si
tienen signo contrario. En caso de que los dos parámetros en
cuestión tengan el mismos valor los puntos extremos coinciden
dando lugar a un punto de inflexion que puede estar en ![]() ,
según los signos de
,
según los signos de ![]() y
y ![]() .
La discusión anterior permite que se tenga una idea acerca de los
tipos de curvas que pueden resultar. Eso se ilustra en las
figuras 1.11.
La función no es simétrica en general, lo es sólo en el caso
de que el parámetro
.
La discusión anterior permite que se tenga una idea acerca de los
tipos de curvas que pueden resultar. Eso se ilustra en las
figuras 1.11.
La función no es simétrica en general, lo es sólo en el caso
de que el parámetro ![]() sea nulo y en esas condiciones la
forma de las curvas es como la de la
Figura 1.12.
sea nulo y en esas condiciones la
forma de las curvas es como la de la
Figura 1.12.