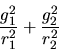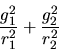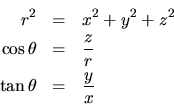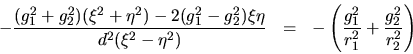Next: Generalidades sobre el monopolo
Up: Introducción
Previous: Otro método
Contents
Vamos a considerar ahora el efecto de omitir los términos:
éstos se deben al paso de coordenadas cartesianas a
elipsoidales, podemos ilustrar este hecho para el caso de un
centro usando coordenadas polares. Se tiene para ese caso:
En esas coordenadas, se tiene para 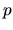 lo siguiente:
lo siguiente:
Entonces si aparece un término de la forma
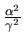 ,
escribimos:
,
escribimos:
Un cambio en el potencial por una cantidad 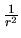 produce un
efecto equivalente a cambiar el momento angular efectivo. Cuando
se considera una trayectoria sin el término
produce un
efecto equivalente a cambiar el momento angular efectivo. Cuando
se considera una trayectoria sin el término 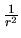 en
el potencial, el movimiento ocurre en un plano, lo que indica que
el momento angular se conserva. Con el nuevo término, veremos
que el incremento del ángulo barrido por el radio vector de la
partícula va a ser modificado en todo momento por una
cantidad dependiente de
en
el potencial, el movimiento ocurre en un plano, lo que indica que
el momento angular se conserva. Con el nuevo término, veremos
que el incremento del ángulo barrido por el radio vector de la
partícula va a ser modificado en todo momento por una
cantidad dependiente de  , la trayectoria precederá
alrededor de un centro; este fenómeno se presenta
independientemente del plano donde ocurra el movimiento. Dicho
resultado es muy antiguo y se conoce como ``Teorema de
Newton'' [23].
Es necesario considerar estos hechos tratándose del monopolo
magnético por la razón de que la trayectoria se desarrolla
sobre la superficie de un cono. Se ha visto que un cono al
desenvolverse sobre la superficie de un plano da lugar a un sector
circular cuyo arco tiene una longitud igual a la circunferencia de
una sección recta del cono. Una trayectoria elíptica sobre
el cono al desenvolverse dará lugar a curvas como la que
indicamos en la Figura 1.13.
, la trayectoria precederá
alrededor de un centro; este fenómeno se presenta
independientemente del plano donde ocurra el movimiento. Dicho
resultado es muy antiguo y se conoce como ``Teorema de
Newton'' [23].
Es necesario considerar estos hechos tratándose del monopolo
magnético por la razón de que la trayectoria se desarrolla
sobre la superficie de un cono. Se ha visto que un cono al
desenvolverse sobre la superficie de un plano da lugar a un sector
circular cuyo arco tiene una longitud igual a la circunferencia de
una sección recta del cono. Una trayectoria elíptica sobre
el cono al desenvolverse dará lugar a curvas como la que
indicamos en la Figura 1.13.
Figure 1.13:
cono desenrollado
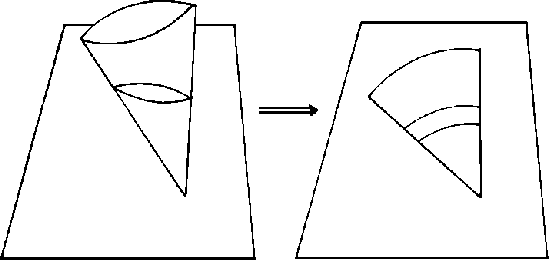 |
No se va a tener una visión completa del movimiento porque
éste, aunque es continuo sobre el cono no lo es sobre el plano.
Se tendrá además una precesión de la órbita (que puede ser
una elipse) de tal manera que el máximo acercamiento ocurre en
diferentes puntos.
Sin entrar en todos los detalles diremos que esa es la motivación
para considerar los términos que hemos mencionado en la energía
cinética. Realmente, al desarrollar (I-3-9) se tenía en la
hamiltoniana un término de la forma:
Este término se omitió para poder separar variables. Dicha
omisión corresponde a sumar a la ecuación (I-4-5) un potencial
centrífugo de la forma 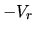 , eso significa que los
resultados van a incluir el efecto producido por dicho potencial,
que como se ha dicho, produce una precesión de las órbitas,
vease la referencia [23].
, eso significa que los
resultados van a incluir el efecto producido por dicho potencial,
que como se ha dicho, produce una precesión de las órbitas,
vease la referencia [23].




Next: Generalidades sobre el monopolo
Up: Introducción
Previous: Otro método
Contents
Pedro Hernandez
2006-02-20