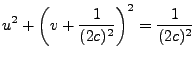Next: Transformaciones conformes
Up: Transformaciones o mapeos
Previous: Rotación
Contents
La inversión tiene la forma general
y lo podemos ver como una multiplicación con un factor fraccionario, por lo que de nuevo es conveniente verla desde la forma polar
esto muestra que
Con esto podemos notar que hay una inverción en la magnitud del vector por lo que sí, por ejemplo, tenemos un punto en el círculo unitario después de la tranformación estará afuera. También se nota que el ángulo de  será igual al de
será igual al de
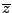 .
.
Si representamos esta transformación con coordenadas cartesianas tendremos
Un círculo con centro en el origen y de radio 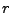 está dado por
está dado por
si substituimos con las ecuaciones ![[*]](file:/usr/share/latex2html/icons/crossref.png) tendremos
simplificando
y esto es un círculo con centro en el origen en el plano
tendremos
simplificando
y esto es un círculo con centro en el origen en el plano 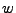 .
.
Si tomamos la línea 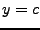
esto representa un círculo en el plano 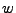 de radio
de radio 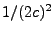 y con centro en
y con centro en
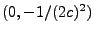 .
.
Existen las posibilidades de que la recta sea positiva (como en éste caso) o negativa, también existe la posibilidad de que la recta en vez de ser horizontal sea vertical, así que en algunos casos nos transformará en rectas o en círculos, como en este caso. En general una inversión transformara círculos y líneas en círculos en líneas, no necesariamente en ese orden.




Next: Transformaciones conformes
Up: Transformaciones o mapeos
Previous: Rotación
Contents
Julio N. Argota Q.
2006-09-28
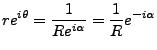
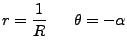
![]() está dado por
está dado por
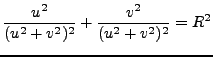
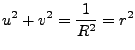
![]()