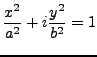Representación polar

Si un número complejo tiene una representación en un plano cartesiano también lo tendrá en un plano polar. Recordando que las ecuaciones para convertir de coordenadas rectangulares a polares y adaptandola al plano de Argand:

$$x = r \cos \theta$$

$$iy = ir \sin \theta$$

donde $r$ es la distancia del origen al punto a través de una línea recta (magnitud del vector) y $\theta$ el ángulo formado por dicha recta y el eje real. A $\theta$ se le conoce como argumento o fase y se denota por Arg($z$) siendo $z$ el número complejo al que corresponde. Sustituyendo las ecuaciones de arriba en la definición de número complejo tendremos

$$z = x + iy = r (\cos \theta + i \sin \theta)$$

y recordando la propiedad de Euler que dice

$$e^{x+iy} = e^x(\cos x + i \sin y)$$

substituyendo tendremos

$$z = x + iy = r e^{i\theta}$$

siendo $\theta$ y $r$ el argumento y el módulo de $z$ respectivamente.

Notando algunas propiedades geométricas de esta representación podemos ver que si dejamos $r$ fijo y variamos $\theta$ en el intervalo $0 \leq \theta \leq 2\pi$ notaremos que se ira formando un círculo de radio $r$ con centro en el origen. Tambien con una desigualdad con el módulo podemos delimitar todos los puntos de un círculo, a esto se le suele llamar disco, por ejemplo, $\vert z\vert<1$ serán todos los puntos que del origen a un punto tienen un módulo menor a $1$, es decir, todos los puntos internos del círculo de radio 1 con centro en el origen.

Con esta representación podemos ver que propiedades de la muliplicación compleja, definamos $z, w \in$ C y $x, y, u, v \in$ R, entonces la multiplicación de $z$ y $w$ quedara definida así

$$z * w = ( a + ib)( u + iv) = au - bv + i(av + bu)$$

pero si la representamos con polares

$$z * w = r e^{i\theta}( Re^{i\Theta}) = Rr(e^{i\Theta}e^{i\theta}) = Rr(e^{i(\theta + \Theta)})$$

lo que nos da a entender que cuando multiplicamos el argumento del vector resultante será la suma de los argumentos de los números multiplicados. El factor $Rr$ hará un alargamiento de los vectores o una contracción si uno de los dos esta entre el cero y uno.

Daremos un ejemplo con REC/C en el que multiplicaremos un número por $i$, por lo antes mencionado dado cualquier número complejo multiplicado por la unidad imaginaria el resultado será el mismo vector pero rotado en sentido contrario a las manecillas del reloj $\pi / 2$ radianes ya que el argumento de $i$ es $\pi / 2$ y su módulo es 1 .

{(
(ZGp $3.5,1.85$ g ZGp Y g Z Gp *g;)
;)}

Veamos si tenemos un número complejo con un módulo 1 y un argumento $\theta$ dado su representación polar sería $e^{i\theta}$ y la de su conjugado sería $e^{-i\theta}$, si la representamos vectorialmente quedaría la figura 4

Figura: Coseno en términos de suma de exponenciales complejos

notamos que ambos tienen el mismo módulo, que es 1, y el resultado sería un real puro, pero no sólo eso por reglas trigonométricas el resultado es $2\cos{\theta}$. Despejando a $\cos\theta$ el resultado es:

$$\cos \theta = \frac {e^{i\theta} + e^{-i\theta}} 2$$

y tenemos que la suma de dos números complejos da un número real lo cual es totalmente congruente. Otra manera e demostrar este resultado es mediante series de Taylor pero es más laboriosa. Si en ves de sumar estos números los restamos notaremos que el resultado es

$$\sin \theta = \frac {e^{i\theta} - e^{-i\theta}} {2i}$$

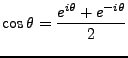
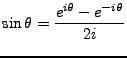
Vemos que la parametrización de un número complejo en su forma polar nos dará como resultado un círculo, pero recordemos que un círculo es un caso especial de una elipse. Para definir una elipse con eje focal en el eje real y centro en el origen

$$\frac {x^2} {a^2} + i\frac {y^2} {b^2} = 1$$

si observamos un poco podemos notar que si sustituimos $x = a\sin\theta$ y $iy =b \cos\theta$ cumple la igualdad. Una parametrización $a\sin\theta + i \cos\theta$ con $0 \leq \theta \leq 2\pi$ nos dará una elipse como resultado. Este resultado no es de mucha trascendencia pero es un buen dato.