Representación matricial

Un número complejo se puede representar como un vector y un vector como matriz,por lo que suena lógico que un número complejo se pueda representar con una matriz, sólo que la representación no tiene que ser propiamente la de un vector en una matriz. Una posible representación de $z \in \mathbb{R}$ con $Re(z) = a$ y $Im(z) = b$

$$z = \left( \begin{array}{ccc} a & b \\ -b & a \end{array}\right)$$

El primer renglón nos dará el número complejo. Podemos definir la unidad real como

$$\left( \begin{array}{cccc} 1 & 0 \\ 0 & 1 \end{array}\right)$$

y la imaginaria como

$$\left( \begin{array}{cccc} 0 & 1 \\ -1 & 0 \end{array}\right)$$

al ser un número complejo la suma de un número real más otro número real por la unidad imaginaria, podemos hacerlo matricialmene

$$z =a \left( \begin{array}{cccc} 1 & 0 \\ 0 & 1 \end{arra... ...ft( \begin{array}{cccc} a & b \\ -b & a \end{array}\right)$$

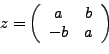
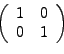
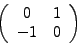
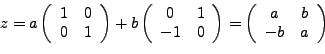
Con esta representación la aritmetica compleja es isomorfa a las operaciones con matrices.