Base de un Espacio Vectorial

Hasta el momento, hemos visto que las relaciones de orden nos ofrecen una forma de organizar los subespacios de un espacio vectorial según su contención, en especial, todos los múltiplos escalares de un subespacio $\mathcal{W}\subseteq \mathcal{V}$ forman el menor conjunto que incluye a $\mathcal{W}$.

Supongamos que para $\mathcal{W}\subseteq \mathcal{V}$, con $\mathcal{W}=\{w_1,w_2,\ldots,w_m\}$, todo elemento $v \in \mathcal{V}$ es una combinación lineal de los elementos de $\mathcal{W}$, es decir:

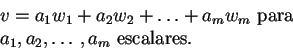$$\begin{array}{l} v=a_1w_1+a_2w_2+\ldots+a_mw_m \mbox{ para } a_1,a_2,\ldots,a_m \mbox{ escalares.} \end{array}$$ (1)

entonces se dice que $\mathcal{V}$ es una expansión de $\mathcal{W}$.

Para $\mathcal{W}=\{w_1,w_2,\ldots,w_m\} \subseteq \mathcal{V}$, decimos que $\mathcal{W}$ es linealmente dependiente si existen escalares $a_1,a_2,\ldots,a_m$ no todos iguales a 0 tal que:

$$a_1w_1+a_2w_2+\ldots+a_mw_m=0.$$ (2)

Esto indica que alguno de los elementos de $\mathcal{W}$ es múltiplo de otro; en caso contrario, si la ecuación 2 no se cumple más que para $a_1=a_2=\ldots=a_m=0$, entonces los elementos de $\mathcal{W}$ son linealmente independientes.

De aquí, si $\mathcal{V}$ es una expansión de $\mathcal{W}$ , entonces el conjunto de vectores linealmente independientes $\mathcal{B}\subseteq \mathcal{W}$ forma una base de $\mathcal{V}$. Con las relaciones de orden sobre $\mathcal{V}$, podemos encontrar $\mathcal{B}$ como el conjunto de elementos linealmente independientes que generan a $\mathcal{V}$ por medio de todas las posibles combinaciones lineales, así, el número de vectores linealmente independiente en $\mathcal{B}$ dado por $\left\vert\mathcal{B}\right\vert$ define la dimensión del espacio.