La definición presentada en esta sección de la teoría del campo promedio se obtuvo del trabajo realizado por Gutowitz en [22], [23] y [25].
La teoría del campo promedio es un modelo simple que proporciona propiedades estadísticas de los autómatas celulares. La teoría del campo promedio se basa en que los elementos del conjunto de estados ![]() son independientes entre si, es decir, no hay correlación entre cada uno de los elementos que se encuentran en el espacio de evoluciones, bajo esta condición es fácil estimar la probabilidad de los estados en una vecindad en términos de la probabilidad de un solo estado (el estado en que evoluciona la vecindad). La probabilidad de la vecindad es el producto de las probabilidades de los estados que forman la vecindad.
son independientes entre si, es decir, no hay correlación entre cada uno de los elementos que se encuentran en el espacio de evoluciones, bajo esta condición es fácil estimar la probabilidad de los estados en una vecindad en términos de la probabilidad de un solo estado (el estado en que evoluciona la vecindad). La probabilidad de la vecindad es el producto de las probabilidades de los estados que forman la vecindad.
La probabilidad de que una célula tenga un estado en particular en el tiempo ![]() , es la suma de las probabilidades de las vecindades que se transforman a este estado en el tiempo
, es la suma de las probabilidades de las vecindades que se transforman a este estado en el tiempo ![]() . Se consideran únicamente las vecindades definidas para el estado de la célula en estudio, porque la regla de evolución es local. Sea
. Se consideran únicamente las vecindades definidas para el estado de la célula en estudio, porque la regla de evolución es local. Sea ![]() la regla de evolución de un autómata celular de orden
la regla de evolución de un autómata celular de orden ![]() con dos estados por célula, por lo tanto
con dos estados por célula, por lo tanto
![]() .
.
La vecindad es de tamaño ![]() ,
, ![]() es el número de vecindades,
es el número de vecindades,
![]() tomará el valor de 0 ó 1 dependiendo de la transformación de cada vecindad para una regla de evolución en particular, la vecindad
tomará el valor de 0 ó 1 dependiendo de la transformación de cada vecindad para una regla de evolución en particular, la vecindad
![]() se representará como
se representará como ![]() . Sea
. Sea ![]() la probabilidad de tener el estado 1 en el tiempo
la probabilidad de tener el estado 1 en el tiempo ![]() ,
, ![]() es la probabilidad de tener el estado 0 en el tiempo
es la probabilidad de tener el estado 0 en el tiempo ![]() ,
, ![]() es el número de veces que aparece el estado 1 en la vecindad,
es el número de veces que aparece el estado 1 en la vecindad, ![]() es el número de veces que aparece el estado 0 en la vecindad, la sumatoria tomará cada una de las vecindades definidas por el conjunto
es el número de veces que aparece el estado 0 en la vecindad, la sumatoria tomará cada una de las vecindades definidas por el conjunto
![]() , entonces la teoría del campo promedio calcula la densidad en el tiempo
, entonces la teoría del campo promedio calcula la densidad en el tiempo ![]() como:
como:
nótese que ![]() es el número de vecindades y
es el número de vecindades y
![]() es el conjunto que define cada una de las vecindades, además la teoría del campo promedio puede ser empleada en autómatas celulares de diferentes dimensiones. Los puntos fijos que representa la teoría del campo promedio son una estimación de la densidad de los estados en un largo tiempo, esta densidad es independiente de la densidad inicial.
es el conjunto que define cada una de las vecindades, además la teoría del campo promedio puede ser empleada en autómatas celulares de diferentes dimensiones. Los puntos fijos que representa la teoría del campo promedio son una estimación de la densidad de los estados en un largo tiempo, esta densidad es independiente de la densidad inicial.
McIntosh hace notar la relación que existe entre la teoría del campo promedio y los polinomios de Bernstein en [44], la definición de los polinomios de Bernstein que se presenta se obtuvo de [37].
Sea una función ![]() definida en el intervalo cerrado
definida en el intervalo cerrado ![]() entonces la expresión:
entonces la expresión:
es llamado el Polinomio de Bernstein de orden ![]() de la función
de la función ![]() .
. ![]() es un polinomio en
es un polinomio en ![]() de grado
de grado ![]() donde
donde
![]() . El polinomio
. El polinomio ![]() sería introducido por S. Bernstein para dar una demostración de la aproximación del teorema de Weierstrass. Pero si
sería introducido por S. Bernstein para dar una demostración de la aproximación del teorema de Weierstrass. Pero si ![]() es continua en
es continua en ![]() , entonces:
, entonces:
| (2.5.3) |
uniformemente en ![]() . Aquí hay muchas otras expresiones llamadas ``integrales singulares'' y la relación que tienen con los polinomios de Bernstein es la aproximación que realizan ``generando'' la función
. Aquí hay muchas otras expresiones llamadas ``integrales singulares'' y la relación que tienen con los polinomios de Bernstein es la aproximación que realizan ``generando'' la función ![]() además de reproducir algunas de sus propiedades. La integral singular mas conocida es la integral de Dirichlet's
además de reproducir algunas de sus propiedades. La integral singular mas conocida es la integral de Dirichlet's
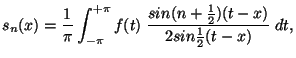
representado las sumas parciales ![]() de las series de Fourier de la función
de las series de Fourier de la función ![]() integrable en
integrable en
![]() . Otro ejemplo es la integral de Fejér que representa la media aritmética
. Otro ejemplo es la integral de Fejér que representa la media aritmética
![]() de
de ![]() . En general una integral singular puede ser escrita en la forma:
. En general una integral singular puede ser escrita en la forma:
donde
![]() es el ``kernel'' definido por
es el ``kernel'' definido por
![]() y
y
![]() , que tiene propiedades de las funciones
, que tiene propiedades de las funciones ![]() de una cierta clase,
de una cierta clase,
![]() converge a
converge a ![]() cuando
cuando
![]() .
.
El polinomio de Bernstein de la Ecuación 2.5.2 es una suma finita de un tipo correspondiente a la integral de la Ecuación 2.5.4. Ambas ecuaciones son casos especiales de la integral de Stieltjes en la variable ![]() ,
,
con el kernel
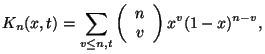 |
(2.5.6) | ||
que es constante en algún intervalo
![]() y tiene el salto
y tiene el salto
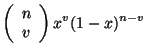
que es el punto básico de la interpolación ![]() . En este sentido la teoría de los polinomios de Bernstein, además de la teoría de las series de Fourier, son un capítulo de la teoría de integrales singulares.
. En este sentido la teoría de los polinomios de Bernstein, además de la teoría de las series de Fourier, son un capítulo de la teoría de integrales singulares.
Los polinomios de Bernstein están conectados con la teoría de la probabilidad, con problemas de momentos y con la teoría de sumas en series divergentes. Un problema complejo e interesante que no ha sido completamente resuelto, concierne a los polinomios de Bernstein en funciones analíticas.
La expresión:
contenida en la Ecuación 2.5.2 es la binomial o las probabilidades de Newton conocidas en la teoría de la probabilidad. Si
![]() es la probabilidad de un evento
es la probabilidad de un evento ![]() , entonces
, entonces
![]() es la probabilidad de que
es la probabilidad de que ![]() debe ocurrir exactemente
debe ocurrir exactemente ![]() veces en
veces en ![]() intentos independientes.
intentos independientes.
La relación que existe entre la teoría del campo promedio y los polinomios de Bernstein se establece entre las Ecuaciones 2.5.1 y 2.5.7. La Ecuación 2.5.1 genera el polinomio completo derivado de todas las evoluciones de cada una de las vecindades, es decir, analiza todos los términos que puede generar la regla de evolución, por otra parte el polinomio de Bernstein de la Ecuación 2.5.7 calcula todas las combinaciones que se pueden generar de un estado en una vecindad de tamaño ![]() , ésto da como resultado un término del polinomio de la Ecuación 2.5.1 en específico para un
, ésto da como resultado un término del polinomio de la Ecuación 2.5.1 en específico para un ![]() y
y ![]() dado, donde
dado, donde ![]() tomará el valor
tomará el valor ![]() y
y ![]() tomará el número de veces que un estado de
tomará el número de veces que un estado de ![]() puede estar en la vecindad, es decir,
puede estar en la vecindad, es decir, ![]() tomará valores entre
tomará valores entre
![]() .
.
Finalmente los polinomios de Bernstein ayudan a no calcular todos los términos posibles del polinomio, como lo hace la teoría del campo promedio, simplemente calculando las combinaciones para un número de veces en que estará un estado en la vecindad, excluyendo todos aquellos términos que no formarán parte del polinomio para una regla de evolución en específico, aunque se sigue empleando la sumatoria pero ahora de binomiales. Esta sumatoria a diferencia de la Ecuación 2.5.1, solo sumará los términos que son calculados por las binomiales.
Para ejemplificar estos conceptos se construye el polinomio de un autómata celular en una dimensión de orden ![]() regla 110. El conjunto de estados
regla 110. El conjunto de estados
![]() , la vecindad es de tamaño
, la vecindad es de tamaño
![]() y el número de vecindades es igual a
y el número de vecindades es igual a
![]() . Entonces la regla de evolución para la regla 110 se representa como:
. Entonces la regla de evolución para la regla 110 se representa como:
|
|
= | 0 |
|
|
= | 1 |
|
|
= | 1 |
|
|
= | 1 |
|
|
= | 0 |
|
|
= | 1 |
|
|
= | 1 |
|
|
= | 0 |
las vecindades son
![]() ,
, ![]() es la probabilidad de obtener el estado 1 en la siguiente generación, el complemento de la probabilidad de
es la probabilidad de obtener el estado 1 en la siguiente generación, el complemento de la probabilidad de ![]() es
es ![]() que es igual a
que es igual a ![]() y
y ![]() es la probabilidad de obtener el estado 0 en la siguiente generación, por lo tanto
es la probabilidad de obtener el estado 0 en la siguiente generación, por lo tanto ![]() donde
donde ![]() y
y ![]() tomarán valores del intervalo cerrado
tomarán valores del intervalo cerrado ![]() .
.
Empleando la Ecuación 2.5.1,
![]() tomará el valor que produzcan las células de evolución para cada una de las vecindades de
tomará el valor que produzcan las células de evolución para cada una de las vecindades de
![]() ,
, ![]() la probabilidad de obtener el estado 1 en la siguiente generación,
la probabilidad de obtener el estado 1 en la siguiente generación, ![]() la probabilidad de obtener el estado 0 en la siguiente generación,
la probabilidad de obtener el estado 0 en la siguiente generación, ![]() es el número de veces que aparece el estado 1 en la vecindad y
es el número de veces que aparece el estado 1 en la vecindad y ![]() es el número de veces que aparece el estado 0 en la vecindad, de esta manera se tiene que:
es el número de veces que aparece el estado 0 en la vecindad, de esta manera se tiene que:
simplificando el polinomio se tiene que:
poniendolo en términos de ![]() y
y ![]() finalemente se obtiene el polinomio de la regla 110:
finalemente se obtiene el polinomio de la regla 110:
como se había mencionado la sumatoria calcula todas las vecindades que deriva la regla de evolución, ahora se emplearán los polinomios de Bernstein de la Ecuación 2.5.7 para ver que resultado produce.
El grado del polinomio ![]() es igual al tamaño de la vecindad, entonces
es igual al tamaño de la vecindad, entonces ![]() y
y ![]() tomará valores de
tomará valores de ![]() que es el número de veces que puede aparecer el estado 1 en la vecindad,
que es el número de veces que puede aparecer el estado 1 en la vecindad, ![]() y
y ![]() .
.
Para ![]() y
y ![]() se tiene:
se tiene:
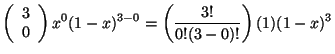 |
|||
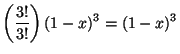 |
en términos de ![]() y
y ![]() finalmente tenemos:
finalmente tenemos:
Para ![]() y
y ![]() se tiene:
se tiene:
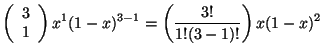 |
|||
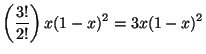 |
en términos de ![]() y
y ![]() finalmente tenemos:
finalmente tenemos:
Para ![]() y
y ![]() se tiene:
se tiene:
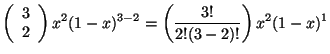 |
|||
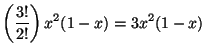 |
en términos de ![]() y
y ![]() finalmente tenemos:
finalmente tenemos:
Para ![]() y
y ![]() se tiene:
se tiene:
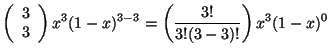 |
|||
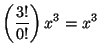 |
en términos de ![]() y
y ![]() finalmente se tiene que:
finalmente se tiene que:
Nótese que los polinomios de Bernstein calculan todos los términos que puede generar el polinomio de la Ecuación 2.5.1, estos términos no toman en cuenta la regla de evolución, sin embargo empleando los dos conceptos se puede simplificar el calculo del polinomio de la teoría del campo promedio para reglas de evolución muy grandes.
La manera en que se simplifica el proceso es calculando los polinomios de Bernstein que determinan la probabilidad de obtener el estado 1 en la siguiente generación, es decir, tomando en cuenta aquellas vecindades que evolucionan al estado 1 y que la suma del estado 1 en cada una de las vecindades correspondan de igual manera, este concepto solo es utilizado para reglas de evolución totalísticas y semitotalísticas. Si las reglas de evolución no fueran de estos dos tipos, entonces se tiene que aplicar la Ecuación 2.5.1 y este método no puede ser aplicado.