



Next: Modelo de arranque lento
Up: Analizando la regla de
Previous: Modelo de Fuks y
Contents
Recientemente se propuso una generalización de la
regla de AC(2,1) 184 con el propósito de aplicarla en el
análisis de diversos fenómenos del transporte a través de la
obtención de varias propiedades algebraicas. Su ecuación de
evolución es
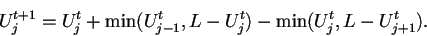 |
(4.2) |
donde 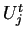 representa un auto en el sitio
representa un auto en el sitio 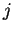 en el tiempo
en el tiempo 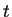 ,
,
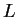 es un entero positivo fijo. Se asume que puede haber
es un entero positivo fijo. Se asume que puede haber 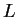 autos
como máximo, es decir, hay
autos
como máximo, es decir, hay 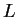 sitios. Podemos comprobar que si
sitios. Podemos comprobar que si
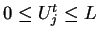 para cualquier
para cualquier 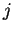 , entonces
, entonces
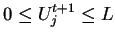 se mantiene para cualquier
se mantiene para cualquier 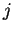 . Debido a
que la ecuación 4.2 se obtiene a partir de
una ultradiscretización de la ecuación de Burgers [33]
a este autómata celular se le conoce como AC Burger (BCA)
[71]. Hay que hacer notar que el BCA es equivalente al
AC(2,1) 184 en el caso en el que
. Debido a
que la ecuación 4.2 se obtiene a partir de
una ultradiscretización de la ecuación de Burgers [33]
a este autómata celular se le conoce como AC Burger (BCA)
[71]. Hay que hacer notar que el BCA es equivalente al
AC(2,1) 184 en el caso en el que 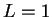 . El entero positivo
. El entero positivo 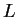 puede interpretarse físicamente como el carril de una
carretera que consta de
puede interpretarse físicamente como el carril de una
carretera que consta de 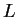 sitios.
sitios.




Next: Modelo de arranque lento
Up: Analizando la regla de
Previous: Modelo de Fuks y
Contents
rene
2003-10-20