



Next: Basados en la teoría
Up: Modelos para flujo de
Previous: Basados en la teoría
Contents
Uno de los campos de la física más complicados
de estudiar son los fluidos, el comportamiento de gases y
líquidos en movimiento. Comprender, por ejemplo, los flujos
de aire turbulento o los remolinos que se forman cuando el agua
discurre por una tubería o la sangre por una arteria son de
suma importancia, tanto para la ingeniería como para la
medicina.
Las ecuaciones que rigen la dinámica de fluidos son
las conocidas como ecuaciones de Navier-Stokes, producto del
francés constructor de puentes Claude-Louis Navier y del
matemá-tico irlandés George Stokes. El primero en obtener estas
ecuaciones fue el francés en una época (1822) en que no se
comprendía muy bien cuál era la física de la
situación que estaba matematizando. De hecho, lo único que
hizo fue modificar unas ecuaciones ya existentes y obtenidas por
el famoso matemático Euler, de modo que incluyesen las fuerzas
existentes entre las moléculas del fluido. Aproximadamente 20
años después, Stokes justificó las ecuaciones del ingeniero
francés deduciéndolas adecuadamente. A pesar de que las
ecuaciones de Navier-Stokes son sólo una aproximación del
comportamiento real de los fluidos, se utilizan para estudiar
cualquier aspecto que tenga que ver con éstos; el problema es
que si uno estudia el movimiento de un fluido con estas
ecuaciones, es incapaz de prever si ese movimiento se va a mantener
siempre o se va a complicar.
Los modelos basados en
la teoría de dinámica de fluídos han sido
desarrollados desde los 1950's y se han utilizado en la ciencia de
tránsito con un éxito considerable. Cuando es visto desde una
gran distancia, por ejemplo, desde un avión, el tránsito
pesado aparece como el torrente de un fluido. Por lo
tanto, un estudio con enfoque macroscópico sobre el flujo
de tránsito de autos se puede desarrollar en analogía con
la teoría hidrodinámica de fluidos tratando al tránsito
como un fluido uni-dimensional de izquierda a derecha.
Sean 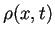 y
y 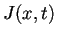 la densidad y el flujo en una
posición arbitraria
la densidad y el flujo en una
posición arbitraria 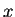 en un instante arbitrario de tiempo
en un instante arbitrario de tiempo 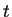 .
La ecuación de continuidad que relaciona a la densidad y el
flujo del tránsito vehicular como un fluido en una carretera
donde no hay ningun tipo
de intersección es:
.
La ecuación de continuidad que relaciona a la densidad y el
flujo del tránsito vehicular como un fluido en una carretera
donde no hay ningun tipo
de intersección es:
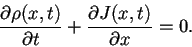 |
(2.1) |
Sin embargo, la ecuación 2.1 no se puede
resolver debido a que existen dos funciones des-conocidas: 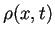 y
y 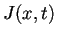 . En uno de los primeros modelos para flujo de
tránsito, Lighthill y Whitham asumen que la función
. En uno de los primeros modelos para flujo de
tránsito, Lighthill y Whitham asumen que la función 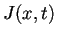 es determinada por la función
es determinada por la función 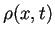 , es decir,
, es decir, 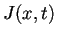 =
= 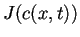 . Insertando esto en la ecuación de continuidad
2.1 se obtiene la ecuación denominada
Lighthill-Whitham
. Insertando esto en la ecuación de continuidad
2.1 se obtiene la ecuación denominada
Lighthill-Whitham
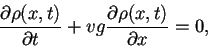 |
(2.2) |
donde
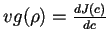 .
.
En los modelos basados en la teoría de dinámica
de fluidos también se contempla la posibilidad de que surgan
atascamientos mediante la incorporación de variables que
representan elementos tales como presión del gas vehicular
y viscosidad. También se incorpora la varianza de
las velocidades como una variable adicional dependiente del espacio
y del tiempo, haciendo una analogía con las ecuaciónes de
Navier-Stokes para fluidos. Con esto se observa un
comportamiento más realista de los atascamientos que se desarrollan.
Al igual que en la teoría cinética, existe un diagrama
fundamental que indica de que manera se comporta el flujo bajo
diferentes concentraciones o densidades.




Next: Basados en la teoría
Up: Modelos para flujo de
Previous: Basados en la teoría
Contents
rene
2003-10-20