



Next: Basados en la teoría
Up: Modelos para flujo de
Previous: Basados en la teoría
Contents
La teoría car-following asume una
relación lineal entre la (re)acción y el estímulo:
acción = sensibilidad

estímulo.
 |
(2.3) |
donde  es la velocidad del i-ésimo auto en una
cadena,
es la velocidad del i-ésimo auto en una
cadena,  es el tiempo necesario para la adaptación (este
tiempo es más grande que el tiempo de reacción), y
es el tiempo necesario para la adaptación (este
tiempo es más grande que el tiempo de reacción), y  es
la distancia hacia el siguiente auto adelante. La mayoría de
las teorías tratan a los vehículos como puntos.
Especialmente en épocas recientes, esta aproximación a brindado nuevos resultados.
es
la distancia hacia el siguiente auto adelante. La mayoría de
las teorías tratan a los vehículos como puntos.
Especialmente en épocas recientes, esta aproximación a brindado nuevos resultados.
Derivando la ecuación 2.3 con respecto al tiempo
nos da

,
donde 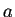 es la aceleración de
es la aceleración de 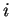 y
y  es la diferencia
de velocidad con respecto al siguiente auto de adelante. Una
generalización tomando en cuenta que la sensibilidad depende de
la distancia y de la velocidad es
es la diferencia
de velocidad con respecto al siguiente auto de adelante. Una
generalización tomando en cuenta que la sensibilidad depende de
la distancia y de la velocidad es
![\begin{displaymath}
a_i (t + \tau) = c_1 \cdot \frac{[v_i (t)]^m}{[\Delta x_i (t)]^l}
\cdot \Delta v_i (t),
\end{displaymath}](img41.gif) |
(2.4) |
donde  y
y  son números enteros. Esta ecuación ha sido
analizada en gran detalle en los 1960's, por ejemplo con respecto
a su estabilidad para un car-following sencillo o para una
cadena infinitamente larga de autos. Uno puede derivar las
relaciones velocidad-densidad y por consiguiente flujo-densidad
desde la ecuación 2.4.
son números enteros. Esta ecuación ha sido
analizada en gran detalle en los 1960's, por ejemplo con respecto
a su estabilidad para un car-following sencillo o para una
cadena infinitamente larga de autos. Uno puede derivar las
relaciones velocidad-densidad y por consiguiente flujo-densidad
desde la ecuación 2.4.
En cualquier
caso, la ecuación 2.4 es problemática para la estimación numérica. Cuando  es cero, la ecuación
permite una distancia arbitrariamente pequeña hacia el auto de
adelante a la vez que permite una velocidad muy alta. En la
teoría, esto nunca pasa en tanto que uno empiece desde
condiciones iniciales realistas, pero debido a la imprecisión
númerica de las simulaciones tales situaciones pueden ocurrir.
es cero, la ecuación
permite una distancia arbitrariamente pequeña hacia el auto de
adelante a la vez que permite una velocidad muy alta. En la
teoría, esto nunca pasa en tanto que uno empiece desde
condiciones iniciales realistas, pero debido a la imprecisión
númerica de las simulaciones tales situaciones pueden ocurrir.
Un modelo basado en la teoría car-following es
el modelo de velocidad óptima (OVM). La ecuación de
aceleración del modelo de velocidad óptima es:
 |
(2.5) |
donde  es una función cuyas características
son
es una función cuyas características
son
 si
si
 y
y
 a cierta distancia de
a cierta distancia de  .
Este modelo ha sido analizado en gran detalle en [2].
Para pequeñas densidades solamente existe una solución homogénea, donde todos los autos se conducen con la misma velocidad.
En una cierta densidad
.
Este modelo ha sido analizado en gran detalle en [2].
Para pequeñas densidades solamente existe una solución homogénea, donde todos los autos se conducen con la misma velocidad.
En una cierta densidad  , esta solución homogénea
se hace linealmente inestable y es cambiada por una solución
donde el sistema tiene varios atascamientos que son separados por
regiones de libre flujo. La densidad
, esta solución homogénea
se hace linealmente inestable y es cambiada por una solución
donde el sistema tiene varios atascamientos que son separados por
regiones de libre flujo. La densidad  de tales
atascamientos es más pequeña que
de tales
atascamientos es más pequeña que  , y por esta
razón una alteración bastante grande puede mover la
intensidad del tránsito desde un régimen de tránsito ligero
a un régimen de tránsito pesado para densidades abajo de
, y por esta
razón una alteración bastante grande puede mover la
intensidad del tránsito desde un régimen de tránsito ligero
a un régimen de tránsito pesado para densidades abajo de
 (pero más grandes que
(pero más grandes que  ).
).
Este modelo es estructuralmente estable, en el sentido de que
pequeños cambios en la ecuación del modelo no cambian su
comportamiento general. Por ejemplo, la introducción
explícita de tiempo de retardo en la ecuación 2.5 da
![\begin{displaymath}
\dot{v}(t) = \alpha [V(\Delta x(t - \tau))-v(t)].
\end{displaymath}](img51.gif) |
(2.6) |
Aunque el retardo cambia el esquema
microscópico en el sentido de que cambia el punto fijo estable
en
 para un cierto rango de velocidades, el
comportamiento macroscópico del modelo no cambia mucho,
como se ha indicado por simulaciones numéricas. En general,
este modelo tiene la desventaja de que no es completamente libre
de choques, un problema que se agrava cuando se utiliza
tiempo de retardo y este despliega aceleraciones muy grandes.
para un cierto rango de velocidades, el
comportamiento macroscópico del modelo no cambia mucho,
como se ha indicado por simulaciones numéricas. En general,
este modelo tiene la desventaja de que no es completamente libre
de choques, un problema que se agrava cuando se utiliza
tiempo de retardo y este despliega aceleraciones muy grandes.
Otro enfoque car-following se basa en observaciones
psicológicas y fisiológicas. Wiedemann [47] repasa este tipo de observaciones antes
de describir una simulación microscópica del modelo
car-following.
Wiedemann considera varios aspectos, uno de ellos es que
la resolución angular del ojo humano es
limitada. Aún cuando un humano puede detectar a un auto que
está acercándose, este puede estimar su velocidad solamente
cuando el auto se hace notablemente grande en su campo de
visión, por ejemplo, cuando el ángulo entre las partes
izquierda y derecha del auto se incrementan. Utilizando
argumentos geométricos, uno puede darse cuenta que este umbral
de observabilidad es proporcional a la diferencia de velocidad, e
inversamente proporcional al cuadrado de la distancia
 |
(2.7) |
Note que esto es similar a la ecuación
2.4 del modelo matemático car-following con  y
y  .
.
De esta manera, después de cruzar el
umbral, la disminución de la velocidad o el frenado se ajusta
con la meta de alcanzar la velocidad del auto de enfrente junto
con un cierto espacio deseado. Medidas consistentes con el
argumento fisiológico indican que el umbral de reacción es
independiente de ciertas velocidades. De esta manera, en algunas
ocasiones el frenar de emergencia puede ser necesario.
Además, la reacción humana para frenar usualmente no
es muy precisa, lo que introduce un elemento altamente estocástico
en el modelo car following.
Resultados más
precisos podrían obtenerse utilizando la psicología
ecológica. La psicología ecológica trata de encontrar
principios generales de cómo los organismos, incluyendo humanos,
interactúan con su ambiente. Las percepciones visuales ligan al
perceptor con su ambiente vía un campo de flujo óptico, el cual
provee la información visual relevante de una determinada
acción.
En el contexto car-following, el
concepto ``tiempo de contacto" es relevante. El tiempo de contacto
ha probado ser un descriptor que informa al perceptor acerca del
movimiento necesario dada una meta. Esta meta podría ser, por
ejemplo, arribar tranquilamente a una posición car-
following deseada.




Next: Basados en la teoría
Up: Modelos para flujo de
Previous: Basados en la teoría
Contents
rene
2003-10-20