Generalizando el Proceso

Usando los conceptos anteriores hemos podido representar la evolución de un autómata celular lineal reversible; sin embargo, la pregunta que se presenta es: ¿este proceso funciona para representar a todo tipo de sistemas de esta clase?. En esta sección trataremos de dar respuesta a dicha cuestión.

Una de las primeras preguntas que surgen es: ¿qué sucede cuando el tamaño de vecindad es par, o sea si el valor de $r$ no es entero?. En el proceso de Kari, se definen las biyecciones $b_L:L_\phi \rightarrow K^{3r}$ y $b_R:R_\phi \rightarrow K^{3r}$, las cuales son fundamentales para definir la permutación en bloque.

Tomemos el siguiente ejemplo, un autómata reversible $(2,1/2)$, es decir de $2$ estados y $r=1/2$, con la regla de evolución $12$ el cual es un corrimiento a la derecha, y cuya regla inversa es la $10$ un corrimiento a la izquierda.

Tabla 4.7: Regla $12$ y $10$ del autómata $(2,1/2)$

Regla 12

Regla 10

	0	1
0	0	0
1	1	1

	0	1
0	0	1
1	1	0

En este caso en que $r=1/2$; el conjunto de $K^{3r}$ estará formado por todas las posibles secuencias de longitud $3r=3(1/2)=3/2$, es decir, secuencias de célula y media de longitud, lo que trae consigo el problema de partir las células. Para solventar este problema, lo que se puede hacer es que en vez de tomar el valor de $r$ para el cual ambas reglas son reversibles, utilizaremos el valor $\lceil r \rceil$, en donde $\lceil r \rceil$ es la función techo de $r$, el menor entero mayor o igual a $r$. Este paso es válido ya que con esto se tomará un valor que es mayor o igual al mínimo $r$ para el cual el autómata es reversible y por lo tanto seguirá cumpliendo con serlo con la ventaja de que $3r$ ya tendrá siempre un valor entero.

En el ejemplo, aplicando $\lceil 1/2 \rceil = 1$, entonces llevemos al autómata reversible $(2,1/2)$ a un autómata $(2,1)$, agregando una célula más a cada vecindad y siguiendo con el comportamiento de corrimiento a la derecha para $\phi$ y de corrimiento a la izquierda para $\phi ^{-1}$ que corresponden a las reglas $240$ y $170$ repectivamente.

Tabla 4.8: Regla $240$ y $170$ del autómata $(2,1)$

Regla 240

Regla 170

	00	01	10	11
00	0	0
01			0	0
10	1	1
11			1	1

	00	01	10	11
00	0	1
01			0	1
10	0	1
11			0	1

Con este cambio, tenemos ahora que el tamaño de las secuencias de el conjunto $K^{3 \lceil r \rceil}$ siempre será entero; pero, observemos las nuevas reglas generadas. La regla original tiene como característica que los valores de sus índice de Welch son $L=1$ y $R=4$, lo cual nos lleva a una segunda pregunta con respecto a la definición de Kari: ¿qué sucede si los índices de Welch son distintos entre sí ?.

Veamos una vez mas como definimos las permutaciones en bloque; cada permutación de un bloque de longitud $6r$ consiste en aplicar a los $3r$ elementos izquierdos la composición $(b_L \circ f_{L_\phi})$ y aplicar a los $3r$ elementos derechos la composición $(b_R \circ f_{R_\phi})$. Sabemos que tanto $b_L$ como $b_R$ mapean de manera biyectiva los elementos de los conjuntos $L_\phi$ y $R_\phi$ al mismo conjunto $K^{3r}$, es decir, ambos conjuntos $L_\phi$ y $R_\phi$ tienen la misma cardinalidad, ya que $\vert L_\phi\vert=Lk^{2r}$ y $\vert R_\phi\vert=Rk^{2r}$, esto indica que $L=R$, o que ambos índices de Welch son iguales.

Tomemos el caso en que esto no ocurra, tendremos que $\vert L_\phi\vert \neq \vert R_\phi\vert$, y las biyecciones $b_L$ y $b_R$ no podrán aplicarse, pongamos como ejemplo el autómata $(2,1)$ anteriormente presentado, el valor de $\vert L_{240}\vert=Lk^{2r}=4$ y $\vert R_{240}\vert=Rk^{2r}=16$, sabemos también que $k^{3r}=2^{3(1)}=8$. Tenemos que el conjunto $L_{240}$ tiene $4$ elementos, el conjunto $R_{240}$ tiene $16$ elementos y el conjunto $K^{3r}$ tiene $8$ elementos; si deseáramos aplicar los mapeos $b_L$ y $b_R$, en el primer caso tenemos que mapear de un conjunto de $4$ elementos a uno de $8$, es decir, nos sobran elementos a mapear en $K^{3r}$, lo cual no puede ser muy importante, pero en el segundo caso, debemos mapear $16$ elementos de un conjunto a otro con sólo $8$ elementos, aquí nos faltan elementos y por lo tanto las permutaciones no se pueden definir.

En la demostración de su teorema, Kari toma el valor del índice $h_-=1$ como base para definir las biyecciones $b_L$ y $b_R$. El que $h_-=1$ indica que a la vez $h_+=1$ ya que $h_-*h_+=1$, recordando que $h_-=\frac{\vert L_\phi\vert}{k^{3r}}$ y $h_+=\frac{\vert R_\phi\vert}{k^{3r}}$.

Entonces, podemos redefinir a los índices $h_-$ y $h_+$, haciendo un uso explícito de los índices de Welch $L$ y $R$, quedando entonces:

$$\begin{array}{ccccc} h_-=\frac{\vert L_\phi\vert}{Lk^{2r}}&&y&&h_+=\frac{\vert R_\phi\vert}{Rk^{2r}} \end{array}$$ (4.10)

Esta pequeña redefinición provoca que tanto $h_-$ como $h_+$ siempre valgan $1$ y por lo tanto, se puedan definir las biyecciones $b_L$ y $b_R$, ahora bien, dichas biyecciones ya no serán hacia el conjunto $K^{3r}$, sino que quedarán definidas como sigue:

$$b_L:L_\phi \rightarrow \mbox{conjunto de secuencias de $K$\ con cardinalidad $Lk^{2r}$}$$ (4.11)

$$b_R:R_\phi \rightarrow \mbox{conjunto de secuencias de $K$\ con cardinalidad $Rk^{2r}$}$$ (4.12)

Debemos señalar con cuidado algo, la definición de $b_L$ y $b_R$ parece ser muy sencilla, sin embargo tienen mucha más relevancia de lo que uno podría suponer a primera vista, el que estas biyecciones vayan al conjunto $K^{3r}$ indica, primero, que la longitud de cada secuencia en este conjunto es de $3r$, y en segunda, indica de que longitud debe ser el corrimiento a realizar entre la primera y la segunda permutación en bloque. Hemos visto que esto funciona muy bien en el caso en donde los índices de Welch $L$ y $R$ son iguales, pero cuando no lo son, $b_L$ y $b_R$ ya no pueden mapear al conjunto $K^{3r}$, sino deben mapear a otros conjuntos de secuencias de $K$ cuyas cardinalidades deben ser $Lk^{2r}$ y $Rk^{2r}$ respectivamente para definir una biyección con $L_\phi$ y $R_\phi$. En principio, la pregunta que planteamos es: ¿qué longitud deben tener entonces las secuencias en ambos conjuntos?.

Tomemos primero el caso izquierdo, para conocer esto debemos poner a la expresión $Lk^{2r}$ en forma de un exponente de $k$, aplicando logaritmos

$$L=k^{\log_kL}$$ (4.13)

resultando

$$Lk^{2r}=k^{\log_kL}k^{2r}=k^{2r+\log_kL}$$ (4.14)

Procediendo de la misma forma para el lado derecho

$$Rk^{2r}=k^{2r+\log_kR}$$ (4.15)

De lo anterior se desprende que la longitud de las secuencias en $L_\phi$ y $R_\phi$ son:

$$2r+\log_kL$$ (4.16)

$$2r+\log_kR$$ (4.17)

respectivamente.

Además, el corrimiento debe tener una longitud de $2r+\log_kL$ entre la primera y la segunda permutación en bloque.

Retomando nuestro ejemplo del autómata $(2,1)$, vemos que los índices de Welch son $L=1$ y $R=4$, con cardinalidades $\vert L_{240}\vert=4$, $\vert R_{240}\vert=16$. De las ecuaciones 4.16 y 4.17 tenemos

$$2r+\log_kL=2(1)+\log_21=2 \mbox{ y } 2r+\log_kR=2(1)+\log_24=4$$ (4.18)

entonces

$$k^{2r+\log_kL}=2^2=4 \mbox{ y } k^{2r+\log_kR}=2^4=16$$ (4.19)

Por consecuencia las biyecciones $b_L:L_{240} \rightarrow K^2$ y $b_R:R_{240} \rightarrow K^4$ están bien definidas al igual que las longitudes de las secuencias tanto para $K^2$ como para $K^4$, siendo $2$ y $4$ respectivamente. Por último, el corrimiento entre la primera y la segunda permutación en bloque debe ser de longitud $2$.

Asignemos el mapeo $b_{L_{240}}$ de la siguiente manera:

Tabla 4.9: Mapeo $b_{L_{240}}$

$\begin{array}{cccc} \begin{array}{ccc} \cline{1-2} \multicolumn{1}{\vert c}{0}... ...multicolumn{1}{c\vert}{1} \\ \cline{2-3} \end{array}\rightarrow 00 \end{array}$

Ahora asignemos el mapeo $b_{R_{240}}$.

Tabla 4.10: Mapeo $b_{R_{240}}$

$\begin{array}{cccc} \begin{array}{ccc} \cline{2-3} \multicolumn{1}{c}{}&\multi... ...}&\multicolumn{1}{c}{} \\ \cline{1-2} \end{array} \rightarrow 1011 \end{array}$

Sabemos que $R_\phi=L_\phi^{-1}$ y que $L_\phi=R_\phi^{-1}$, es decir, podemos obtener a $L_{170}$ y a $R_{170}$ por medio de $R_{240}$ y $L_{240}$ respectivamente, esto se hace intercambiando la posición de los bloques en cada elemento de $R_{240}$ y de $L_{240}$, por supuesto, se deben conservar los mismos mapeos $b_L$ y $b_R$; basándonos en la biyección $b_L$ en $L_{240}$, asignemos ésta misma al conjunto $R_{170}$.

Tabla 4.11: Mapeo $b_{R_{170}}$

$\begin{array}{cccc} \begin{array}{ccc} \cline{2-3} \multicolumn{1}{c}{}&\multi... ...}{1}&\multicolumn{1}{c}{} \\ \cline{1-2} \end{array}\rightarrow 00 \end{array}$

Por último, asignemos $b_R$ en $R_{240}$ a $L_{170}$.

Tabla 4.12: Mapeo $b_{L_{170}}$

$\begin{array}{cccc} \begin{array}{ccc} \cline{1-2} \multicolumn{1}{\vert c}{0}... ...ticolumn{1}{c\vert}{1} \\ \cline{2-3} \end{array} \rightarrow 1011 \end{array}$

El proceso funcionará de la siguiente manera, tomemos una secuencia de estados y veamos como evoluciona bajo la regla $240$.

Figura 4.12: Evolución de un autómata $(2,1)$ regla $240$

Observamos el típico comportamiento de un corrimiento a la derecha, ya tenemos una configuración inicial y conocemos su evolución, veamos si llegamos al mismo resultado utilizando la nueva definición de las biyecciones, apliquemos a la configuiración inicial la permutación en bloque $p_1$.

Figura 4.13: Permutación en bloque $p_1$ sobre la configuración inicial

Así hemos obtenido una nueva secuencia de estados, a continuación apliquemos a esta secuencia la permutación $p_2^{-1}$ con un corrimiento de tamaño 2.

Figura 4.14: Permutación $p_2^{-1}$ con un corrimiento de tamaño $2$

En la Figura 4.14 se observa que al aplicar $p_2^{-1}$ los bloques de tamaño $2$ generan construcciones de longitud $3$ ocurriendo lo mismo para los bloques de tamaño $4$. Por consecuencia las biyecciones se tienen que realinear para conservar la simetría con las permutaciones en bloque de $p_1$.

Al final se ha obtenido una secuencia la cual concuerda con la evolución de la configuración inicial bajo la regla $240$; entonces el resultado de este proceso ha sido poder representar la evolución de este autómata $(2,1)$ como la composición de dos permutaciones en bloque $p_1 \circ p_2^{-1}$, pero redefiniendo $b_L:L_\phi \rightarrow K^{2r+{\log_kL}}$ y $b_R:R_\phi \rightarrow K^{2r+{\log_kR}}$ y con un corrimiento entre ambas permutaciones de tamaño $2r+\log_kL$.

Figura: Funcionamiento de un autómata $(2,1)$ regla $240$ por medio de dos permutaciones en bloque

En la Figura 4.15 se observa de manera simplificada este proceso en donde las permutaciones $p_1$ aparece de color negro y las permutaciones $p_2^{-1}$ en color gris.

Las redefiniciones hechas anteriormente han brindado al proceso de Kari una generalidad mayor, sin embargo, propongamos el siguiente escenario; tomemos un autómata celular lineal reversible $(6,1)$, en el cual se cumple que $k^{2r}=6^2=36$; por lo tanto, valores factibles de los índices de Welch pueden ser $L=4$ y $R=9$, hemos dicho que la expresión $2r+\log_kL$ define tanto la longitud de las secuencias en que se van a mapear los elementos de $L_\phi$ bajo $b_L$ así como el tamaño del corrimiento entre las permutaciones en bloque, retomando el ejemplo, si sustituimos $k$, $r$ y $L$ en la expresión obtenemos que el resultado es $2(1)+\log_64=2.7737056$.

El valor obtenido es correcto, el conjunto $L_\phi$ tendrá tantos elementos como $Lk^{2r}=4*6^{2(1)}=144$, si no exite ninguna equivocación esto debe ser igual a $k^{2r+{\log_kL}}$, sustituyamos los valores, encontramos que $6^{2.7737056}=144$, sin embargo, no podemos representar secuencias de longitud $2.7737056$ ni podemos hacer un corrimiento de ese tamaño en un espacio discreto donde el autómata celular se desenvuelve, entonces, aunque analíticamente no hay error, es imposible representar todos los autómatas celulares lineales reversibles con estas redefiniciones.

Se podría pensar en utilizar nuevamente $\lceil 2r+\log_kL \rceil$ para hacer entero este valor, sin embargo, en algunos casos tendríamos el problema de que las permutaciones serían de bloques de tamaño $6r$ a bloques de una longitud mayor, trayendo consigo problemas de realineación entre las permutaciones en bloque para representar correctamente la evolución del autómata.

Otra posible solución entonces sería llevar a todo autómata reversible a una forma en donde sus índices de Welch sean iguales, y el valor de $r$ sea entero para poder utilizar el proceso descrito por Kari sin modificación alguna, esto podría hacerse tomando valores de $r$ más grandes que el inicial de ser necesario, o haciendo productos cartesiano de la regla de evolución original con su reflexión para igualar los índices de Welch, por supuesto, esto trae los inconvenientes de manejar un mayor tamaño de vecindad y/o un mayor número de estados, pero es factible en teoría.

El problema que se ha visto con las redefiniciones es que, ni la longitud de las secuencias ni el corrimiento son siempre representables. Esto se debe por una parte a que las biyecciones $b_L$ y $b_R$ mapean $L_\phi$ y $R_\phi$ al conjunto $K^{nl}$ y $K^{nr}$ respectivamente, los cuales no siempre pueden formar secuencias de longitud exactamente igual a $nl$ o $nr$ según corresponda. Tampoco es posible aplicar siempre un corrimiento entre las permutaciones en bloque de tamaño $nl$. Si es así entonces surge la pregunta: ¿por qué no tomar otros conjuntos a donde mapear $L_\phi$ y $R_\phi$?.

La importancia de este proceso radica en las diferencias de los ancestros que guardan $L_\phi$ y $R_\phi$ en un autómata reversible; es decir, contabilizan de alguna forma los índices de Welch, y las biyecciones $b_L$ y $b_R$ solo enumeran dichos conjuntos, pero hemos visto que hasta ahora la manera de enumerarlos no siempre es factible por medio de secuencias del conjunto $K$, entonces busquemos enumerarlos de alguna otra forma que siempre sea factible.

Definamos los siguientes conjuntos:

$$X=\{ x_0, x_1,...,x_{(Lk^{2r}-1)}\}$$ (4.20)

$$Y=\{ y_0, y_1,...,y_{(Rk^{2r}-1)}\}$$ (4.21)

claramente, $\vert L_\phi\vert=\vert X\vert$ y $\vert R_\phi\vert=\vert Y\vert$; tomemos nuevamente las definiciones de $h_-$ y $h_+$ como:

$$\begin{array}{ccccc} h_-=\frac{\vert L_\phi\vert}{Lk^{2r}}&&y&&h_+=\frac{\vert R_\phi\vert}{Rk^{2r}} \end{array}$$ (4.22)

Volvamos al resultado de Kari y reescribamos su prueba.

Kari 2   (Resultado (3.3)) Cada autómata celular lineal reversible en el kernel de $h_-$ es una composición de dos permutaciones en bloque.

Prueba: Considere a $r$ tal que representa a las vecinades de $\phi$ y $\phi ^{-1}$. Debido a que $\vert L_\phi\vert=\vert X\vert$ y $\vert R_\phi\vert=\vert Y\vert$, las biyecciones

$$b_L:L_\phi \rightarrow X$$ (4.23)

$$y$$

$$b_R:R_\phi \rightarrow Y$$ (4.24)

existen, el mapeo puede ser cualquiera siempre y cuando cumpla con ser biyectivo.

Ahora bien, si consideramos

$$\begin{array}{c} f_{L_\phi}:K^{6r} \rightarrow L_\phi \\ y \\ f_{R_\phi}:K^{6r} \rightarrow R_\phi \end{array}$$

como ya han definido en la sección 4.2 y sean

$$\begin{array}{c} f_{L_{\phi^{-1}}}:K^{6r} \rightarrow L_{\ph... ...i^{-1}}}:K^{6r} \rightarrow R_{\phi^{-1}} = L_\phi \end{array}$$

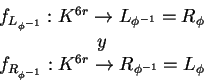
las funciones correspondientes para la regla inversa $\phi ^{-1}$.

Tanto con las funciones para $\phi$ como para $\phi ^{-1}$ nosotros podemos encontrar las permutaciones $\pi _1$ y $\pi _2$ de $K^{6r}$ dados por:

$$\pi_1(c_0,...,c_{6r-1})=[(b_L \circ f_{L_\phi})(c_0,...,c_{6r-1}),(b_R \circ f_{R_\phi})(c_0,...,c_{6r-1})]$$ (4.25)

$$\pi_2(c_0,...,c_{6r-1})=[(b_R \circ f_{L_{\phi^{-1}}})(c_0,...,c_{6r-1}),(b_L \circ f_{R_{\phi^{-1}}})(c_0,...,c_{6r-1})]$$ (4.26)

Obteniendo una evolución de un autómata reversible.

Figura 4.16: Evolución de un autómata reversible por medio de dos permutaciones en bloque y un corrimiento de tamaño $1$

Cada elemento en $X$ y $y$ representa a una longitud $3r$.

$P_1$ resulta ser la permutación en bloque definida para un bloque de tamaño $6r$ en la primera configuración de estados, aplicándole a este bloque la permutación $\pi _1$. $P_2$ es la permutación en bloque definida para un bloque de tamaño $6r$ en la segunda configuración y haciendo un corrimiento de longitud $1$ en la secuencia $\{x_iy_j...x_my_n\}$ correspondiente a un corrimiento de longitud $3r$ en la segunda configuración.

Entonces tenemos que $\phi=p_2^{-1} \circ p_1$. $\blacksquare$