Proceso de Kari

La sección tres del trabajo de Kari [Kari 96] nos dice que todo autómata celular lineal reversible puede ser generado por medio de permutaciones en bloque y corrimiento parciales. Nosotros en esta sección daremos un paráfrasis del resultado de Kari, mediante el ejemplo del autómata reversible $(2,1)$ regla $204$, visualizando paso a paso algunos resultados parciales que encontramos en el proceso.

El autómata reversible $(2,1)$ regla $204$ tiene la siguiente evolución.

Figura 4.1: Autómata $(2,1)$ regla $204$

La regla de evolución $204$ es la siguiente.

Tabla 4.1: Regla de evolución $204$ de un autómata $(2,1)$

	00	01	10	11
00	0	0
01			1	1
10	0	0
11			1	1

Como se puede observar en la Figura 4.1 la regla de evolución consiste en copiar el elemento central de la vecindad, por lo que a esta regla también se le conoce como la regla identidad.

La multiplicidad uniforme nos dice que cada secuencia tendrá tantos ancestros como $k^{2r}=2^2=4$; los valores de los índices de Welch de esta regla de evolución son $L=2$ y $R=2$, cumpliendo con que $LR=k^{2r}=4$. Además, tenemos que la regla inversa es la misma regla $204$ debido a que solo se copia el elemento central de la vecindad.

Vamos a empezar ahora con la selección del radio de vecindad. Sabemos que si un autómata es reversible, para un radio de vecindad $r$, éste lo seguirá siendo para otros radios de vecindad mayores que $r$. De esta manera, seleccionaremos el valor de $r$ mayor, entre la regla original $\phi$ y la regla inversa $\phi ^{-1}$, teniendo la seguridad que para ambos casos la reversibilidad se mantendrá. En el ejemplo como tanto la regla original como la inversa es la misma, entonces $r=1$.

Para la regla original $\phi$, definamos ahora dos conjuntos, el $L_\phi$ y el $R_\phi$. Estos se forman con todas las posibles cadenas de tamaño $2r$ y las terminaciones izquierdas y derechas respectivamente de todos los posibles ancestros de cada cadena, siendo cada una de estas terminaciones también de tamaño $2r$.

Para obtener dichos conjuntos $L_\phi$ y $R_\phi$, formemos todas aquellas secuencias posibles de tamaño $6r$, para obtener posteriormente su evolución, la cual será una secuencia de tamaño $4r$. Finalmente tomaremos de dichas secuencias los siguientes elementos según indiquen $f_{L_\phi}$ y $f_{R_\phi}$.

Figura 4.2: Elementos de $L_\phi$ y $R_\phi$

Sabemos que dicho autómata es reversible con un radio de vecindad $r$; de este modo, si un bloque de tamaño $2r+1$ define una única célula central en sus ancestros, un bloque de tamaño $4r$ define a su vez un único bloque central de tamaño $2r$ en sus ancestros, dejando las discrepancias de los mismos en los extremos, dichas diferencias estarán contenidas en los conjuntos $L_\phi$ y $R_\phi$.

Del ejemplo tomemos todas las secuencias de tamaño $4r$, es decir, de 4 células y sus ancestros.

Tabla 4.2: Ancestros de las secuencias de longitud $4$

000000 000001 100000 100001 0000	000010 000011 100010 100011 0001	000100 000101 100100 100101 0010	000110 000111 100110 100111 0011	001000 001001 101000 101001 0100	001010 001011 101010 101011 0101	001100 001101 101100 101101 0110	001110 001111 101110 101111 0111
010000 010001 110000 110001 1000	010010 010011 110010 110011 1001	010100 010101 110100 110101 1010	010110 010111 110110 110111 1011	011000 011001 111000 111001 1100	011010 011011 111010 111011 1101	011100 011101 111100 111101 1110	011110 011111 111110 111111 1111

Ahora de estas secuencias obtengamos los conjuntos $L_\phi$ y $R_\phi$.

Tabla 4.3: Conjuntos $L_{204}$ y $R_{204}$

$L_\phi=\left\{ \begin{array}{cccc} \begin{array}{ccc} \cline{1-2} \multicolumn... ...}{1}&\multicolumn{1}{c\vert}{1} \\ \cline{2-3} \end{array}\end{array}\right\}$

$R_\phi=\left\{ \begin{array}{cccc} \begin{array}{ccc} \cline{2-3} \multicolumn... ...c\vert}{1}&\multicolumn{1}{c}{} \\ \cline{1-2} \end{array}\end{array}\right\}$

En este punto, en el cual nos encontramos, el primer resultado que vamos a parafrasear es el (Lema 3.1) de [Kari 96] en el que señala que $\vert L_\phi\vert\vert R_\phi\vert=k^{6r}$.

Los conjuntos $L_\phi$ y $R_\phi$ se obtuvieron de las secuencias de tamaño $4r$ y sus ancestros, existiendo tantas secuencias distintas de esta forma como $k^{4r}$. Debido a que el autómata es reversible cumple con el principio de multiplicidad uniforme y cada una de estas secuencias tiene $k^{2r}$ ancestros, dando como resultado un total de $k^{4r}k^{2r}=k^{6r}$ construcciones de este tipo.

Como se menciono anteriormente, cada bloque de tamaño $4r$ tienen en sus ancestros una única parte central de tamaño $2r$, dejando las diferencias en sus partes izquierdas y derechas, cuantificadas por los índices $L$ y $R$ respectivamente. Por medio de $f_{L_\phi}$ y $f_{R_\phi}$ obtenemos los conjuntos $L_\phi$ y $R_\phi$, formados por bloques de tamaño $2r$ y los extremos de sus ancestros también de tamaño $2r$.

En el caso de $L_\phi$ existen tantos bloques de tamaño $2r$ como $k^{2r}$ y tantos extremos diferentes de ancestros como $L$; teniéndose lo mismo en el caso análogo $R_\phi$. Con lo que respecta a la cardinalidad de estos conjuntos está dada por

$$\vert L_\phi\vert=Lk^{2r} \mbox{ y } \vert R_\phi\vert=Rk^{2r}$$ (4.1)

multiplicando

$$\vert L_\phi\vert\vert R_\phi\vert=Lk^{2r}Rk^{2r}=LRk^{4r}$$ (4.2)

Debido a que el autómata es reversible $LR=k^2r$ por lo que:

$$LRk^{4r}=k^{2r}k^{4r}=k^{6r}$$ (4.3)

justamente lo que Kari señala.

En el ejemplo del autómata $(2,1)$ vemos que $\vert L_\phi\vert=8$, $\vert R_\phi\vert=8$, obteniendo $64$ con el producto $\vert L_\phi\vert\vert R_\phi\vert$. Justamente es el resultado que dá Kari con $k^{6r}=2^6=64$.

Kari define dos indices $h_-$ y $h_+$, que se pueden tomar como una normalización de $\vert L_\phi\vert$ y $\vert R_\phi\vert$ respectivamente.

$$\begin{array}{ccccc} h_-=\frac{\vert L_\phi\vert}{k^3r}&&y&&h_+=\frac{\vert R_\phi\vert}{k^3r} \end{array}$$ (4.4)

Se puede observar que uno es el recíproco del otro.

$$h_-*h_+=\frac{\vert L_\phi\vert R_\phi\vert}{k^{3r}k^{3r}}=\frac{k^6r}{k^6r}=1$$ (4.5)

El segundo resultado importante de Kari es el (Lema 3.2), señalando que

$$h_+(\phi \circ \psi)=h_+(\phi)*h_+(\psi)$$ (4.6)

para dos reglas de evolución reversibles $\phi$ y $\psi$ en un autómata celular; siendo esto igual para $h_-$. Esto es fácil de ver en el siguiente diagrama:

Figura 4.3: Composición de dos reglas de evolución

Observamos en la Figura 4.3 que mientras la primera y la segunda línea son miembros del conjunto $R_\phi$, la segunda y tercer línea son miembros de $R_\psi$. Sin embargo, los bloques en gris claro, son determinados de manera única por el segundo bloque ya que son reglas reversibles; lo que significa finalmente que solo depende de $h_+(\phi)*h_-(\psi)$.

Mostremos esto con el autómata $(2,1)$ regla $204$ como $\phi$ y otro autómata reversible $(2,1)$ regla $15$, como $\psi$.

Tabla 4.4: Regla $204$ y $15$ del autómata $(2,1)$

Regla 204

Regla 15

	00	01	10	11
00	0	0
01			1	1
10	0	0
11			1	1

	00	01	10	11
00	1	1
01			1	1
10	0	0
11			0	0

Observemos en detalle como hacen evolucionar en composición ambas reglas un secuencia de estados.

Figura 4.4: Composición de las reglas 204 y 15 en el autómata $(2,1)$

Analizando la Figura 4.4, para formar un elemento $R_{204,15}$ primero de la secuencia inicial, tomaremos en cuenta dos bloques de tamaño $2r$ con dos bloques de la segunda secuencia; producto de aplicar la regla $204$ con la $15$, obteniendo dos elementos del conjunto $R_{204}$. Después, estos dos bloques junto con otros dos de igual longitud de la última línea, son elementos de $R_{15}$. Los dos bloques en la segunda línea tienen definidos de manera única a los bloques con fondo gris tanto en la primera y tercer línea. Lo anterior debido a que la longitud de estos dos bloques les permite tener una única parte central en sus ancestros tanto en el sentido original como en el inverso y que estos ancestros muestren sus diferencias a los extremos, de lado derecho en los bloques con margen negro y del lado izquierdo con los bloques con margen gris.

Tomando estos resultados preliminares como base, llegamos al resultado más importante del trabajo de Kari [Kari 96].

Kari 1   (Resultado (3.3)) Cada autómata celular lineal reversible en el kernel de $h_-$ es una composición de dos permutaciones en bloque.

Definamos una permutación en bloque dada como $p=(B_t^{(n)})^{-1} \circ \hat{\pi} \circ B_t^{(n)}$. $B_t^n$ primero divide la configuración en secuencias de longitud $n$, empezando en la posición $t$; posteriormente mediante la composición aplicamos la permutación $\pi$ a cada secuencia (donde Kari denota la aplicación de $\pi$ con $\hat{\pi}$) obteniendo una nueva configuración de estados.

La prueba se basa en que el valor de $h_-=1$ establece que los conjuntos $R_\phi$ y $L_\phi$ tienen el mismo número de elementos el cual es $k^{3r}$, por lo que cual podemos definir cualquier tipo de biyecciones

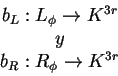$$\begin{array}{c} b_L:L_\phi \rightarrow K^{3r} \\ y \\ b_R:R_\phi \rightarrow K^{3r} \end{array}$$ (4.7)

Las permutaciones estarán dadas de la siguiente manera:

$$\pi_1(c_0,\ldots,c_{6r-1})=[(b_L \circ f_{L_\phi})(c_0,\ldots,c_{6r-1}),(b_R \circ f_{R_\phi})(c_0,\ldots,c_{6r-1}]$$ (4.8)

$$\pi_2(c_0,\ldots,c_{6r-1})=[(b_L \circ f_{L_\phi^{-1}})(c_0,\ldots,c_{6r-1}),(b_R \circ f_{R_\phi^{-1}})(c_0,\ldots,c_{6r-1}]$$ (4.9)

Es decir, realizar cada una de ellas será una composición en donde primero se aplica a cada secuencia de tamaño $6r$ las funciones $f_{L_\phi}$ y $f_{R_\phi}$, después, cada miembro de $L_\phi$ y $R_\phi$ se mapea con la biyección que se haya estipulado en $b_L$ y $b_R$ respectivamente. En síntesis, la permutación $\pi$ mapea una secuencia de estados de tamaño $6r$ a otra secuencia del mismo tamaño formada por dos elementos de $K^{3r}$ y queda representada en la Figura 4.5.

Figura 4.5: Permutación $\pi$ de un bloque de tamaño $6r$

Entonces, en la evolución de un autómata reversible el paso de una configuración a otra por la regla de evolución puede ser definido por dos permutaciones en bloque, la primera, $p_1=(B_t^{(6r)})^{-1} \circ \hat{\pi_1} \circ B_t^{(6r)}$, la cual divide la configuración antecesora en bloques de tamaño $6r$, empezando desde la posición $0$ y aplicando a cada bloque la permutación $\pi _1$. Y la segunda permutación, $p_2=(B_{3r}^{(6r)})^{-1} \circ \hat{\pi_2} \circ B_{3r}^{(6r)}$, la cual divide la configuración sucesora en bloques de tamaño $6r$, empezando desde la posición $3r$ y aplicando a cada bloque la permutación $\pi _2$.

Al final en ambos casos, las permutaciones coinciden en parte con un desfase de $3r$ posiciones (bloque gris en la Figura 4.6), aplicándolas desde el sentido original y el inverso. El mapeo global entre configuraciones inducido por la regla de evolución $\phi$ puede representarse como la composición de dos permutaciones en bloque $p_1 \circ p_2^{-1}$.

Figura 4.6: Representación del funcionamiento de un autómata reversible por medio de dos permutaciones en bloque y un corrimiento

Veamos este proceso tomando el autómata $(2,1)$ regla $204$. Primero formemos $b_L$ asignando al conjunto $L_\phi$ un mapeo biyectivo con el conjunto $K^{3r}$; como la regla de evolución original y la inversa es la misma, ambas tienen los mismos conjuntos $L_\phi$ y $R_\phi$; además, tenemos que se cumple que $L_\phi=R_\phi^{-1}$ y $R_\phi=L_\phi^{-1}$, por lo que $L_\phi=R_\phi$ para este caso. De este modo, dado el mapeo $b_L$, el mapeo $b_R$ queda definido al mismo tiempo.

Tabla 4.5: Mapeo $b_L$ y $b_R$ para el autómata $(2,1)$ regla $204$

$\begin{array}{cccc} \mbox{\small$b_L$}&&&\mbox{\small$b_R$} \\ \\ \begin{arra... ...} \hline 0&0&1 \\ \hline \end{array} \\ && \\ \hline \end{array}\end{array}$

Tomemos ahora una configuración inicial cualquiera y su evolución con la regla $204$.

Figura 4.7: Evolución de un autómata $(2,1)$ regla $204$

Apliquemos ahora las permutaciones $p_1$ y $p_2$, es decir, dividamos dichas configuraciones en bloques de tamaño $6r$, en este caso en bloques de longitud $6$; posteriormente hacemos un corrimiento de estas divisiones entre la primera y segunda configuración de tamaño $3r$ o de tamaño $3$. Por último apliquemos a cada bloque de la primera configuración la permutación $\pi _1$ y a cada bloque de la segunda configuración la permutación $\pi _2$.

Figura 4.8: Funcionamiento de las permutaciones en bloque en el autómata $(2,1)$ regla $204$

Hagamos más claro este proceso, asignemos a cada posible configuración de tamaño $6r$ sus permutaciones correspondientes a $\pi _1$ y $\pi _2$, dado que en este autómata las reglas de evolución original e inversa son idénticas, las permutaciones $\pi _1$ y $\pi _2$ lo son también, por lo que basta enumerar sólo una de ellas.

Tabla 4.6: Permutaciones $\pi _1$ y $\pi _2$ para la regla $204$

$\begin{array}{cccc} \begin{array}{\vert c\vert c\vert c\vert} \hline Bloque&&\... ...tarrow&000011\\ 111111&\leftrightarrow&000001\\ \hline \end{array}\end{array}$

Tomemos una configuración inicial aleatoria, dividamos esta en bloques de tamaño $6$ y permutemos cada bloque como lo indica $\pi _1$.

Figura 4.9: Aplicando $p_1$ a una configuración inicial aleatoria

Hemos obtenido una nueva configuración resultado de las permutaciones de cada bloque. Esta nueva configuración la dividimos también en bloques de tamaño $6$ pero empezando ahora $3$ posiciones más a la derecha de donde comenzamos a dividir la configuración inicial y a cada bloque resultante lo permutamos como indica $p_2^{-1}$.

Figura 4.10: Aplicando $p_2^{-1}$ después de $p_1$ con un corrimiento de $3$ posiciones

Por último, observemos la configuración inicial y la configuración producida al aplicar las permutaciones en bloque $p_1$ y $p_2^{-1}$.

Figura 4.11: Evolución final producida por dos permutaciones en bloque

Como podemos verificar, esta construcción corresponde a la evolución de la configuración inicial bajo la regla $204$; es decir, hemos podido representar dicha evolución por medio de corrimientos y permutaciones en bloque, siguiendo el proceso descrito por Kari.