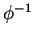 de las Permutaciones
de las Permutaciones 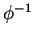 de las Permutaciones
de las Permutaciones
Hasta ahora hemos visto que propiedades deben cumplir las permutaciones ![]() en un autómata reversible, veamos entonces como se puede obtener la regla inversa
en un autómata reversible, veamos entonces como se puede obtener la regla inversa ![]() de una permutación
de una permutación ![]() dada. Usemos como referencia los bloques correspondientes tanto a
dada. Usemos como referencia los bloques correspondientes tanto a ![]() como a
como a ![]() descritos en la Figura 5.5.
descritos en la Figura 5.5.
Para la regla inversa ![]() el papel de estas posiciones se intercambia. Es decir, en los bloques de
el papel de estas posiciones se intercambia. Es decir, en los bloques de ![]() , lo que era la parte izquierda del ancestro ahora es la evolución derecha y, lo que era la parte de la evolución izquierda, pasa a ser la parte derecha del ancestro. En los bloques de
, lo que era la parte izquierda del ancestro ahora es la evolución derecha y, lo que era la parte de la evolución izquierda, pasa a ser la parte derecha del ancestro. En los bloques de ![]() , lo que era la parte derecha del ancestro ahora actua como evolución izquierda y lo que era evolución derecha actuará como parte izquierda del ancestro.
, lo que era la parte derecha del ancestro ahora actua como evolución izquierda y lo que era evolución derecha actuará como parte izquierda del ancestro.
Entonces, podemos hacer particiones en el conjunto ![]() , en donde los elementos de cada partición coincidan en la posición
, en donde los elementos de cada partición coincidan en la posición ![]() ; y del mismo modo podemos particionar el conjunto
; y del mismo modo podemos particionar el conjunto ![]() en donde los elementos de cada partición coincidan en la posición
en donde los elementos de cada partición coincidan en la posición ![]() . En ambos casos tendremos
. En ambos casos tendremos ![]() particiones pues en estas posiciones se encuentran todos los elementos de
particiones pues en estas posiciones se encuentran todos los elementos de ![]() .
Sea
.
Sea ![]() un estado del autómata, para cada partición
un estado del autómata, para cada partición ![]() en
en ![]() se tendrán
se tendrán ![]() elementos distintos en la posición
elementos distintos en la posición ![]() ; que son al mismo tiempo elementos de la posición
; que son al mismo tiempo elementos de la posición ![]() en
en ![]() , sabiendo que el indice de Welch derecho de
, sabiendo que el indice de Welch derecho de ![]() es igual a
es igual a ![]() . De esta manera para cada partición
. De esta manera para cada partición ![]() formemos el conjunto
formemos el conjunto ![]() con los elementos en
con los elementos en ![]() . De manera análoga, para cada partición
. De manera análoga, para cada partición ![]() en
en ![]() se tendrán
se tendrán ![]() elementos distintos en
elementos distintos en ![]() que a su vez es
que a su vez es ![]() , tomemos estos y formemos el conjunto
, tomemos estos y formemos el conjunto ![]() con los elementos en
con los elementos en ![]() .
.
Con estas particiones podemos entonces formar a ![]() , para
, para ![]() , en la regla inversa cada estado
, en la regla inversa cada estado ![]() tendrá
tendrá ![]() estados izquierdos ancestros especificados en
estados izquierdos ancestros especificados en ![]() y
y ![]() estados derechos ancestros especificados en
estados derechos ancestros especificados en ![]() , entonces, la concatenación de todos los elementos del conjunto
, entonces, la concatenación de todos los elementos del conjunto ![]() con todos los elementos del conjunto
con todos los elementos del conjunto ![]() nos darán todas las vecindades ancestras del estado
nos darán todas las vecindades ancestras del estado ![]() .
.