



Next: Caso , ,
Up: Casos de Estudio
Previous: Caso , ,
Contenido
Para este caso tenemos los siguientes ejemplos:
Tabla:
Autómata 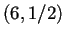 regla original
regla original
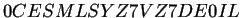 y regla inversa
y regla inversa
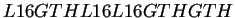
|
|
Las permutaciones son las siguientes:
Tabla 5.18:
Permutaciones 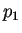 y
y 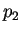 del autómata
del autómata 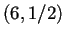
|
|
Los diagramas de Welch de este autómata son:
Figura:
Diagramas de Welch del autómata reversible 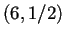 regla
regla
|
|
Tomando una configuración, veamos su evolución normal y por permutaciones en bloque.
Figura 5.15:
Evolución del autómata celular reversible 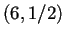 regla
regla
 aplicando
aplicando 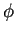 y utilizando las permutaciones en bloque
y utilizando las permutaciones en bloque 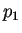 y
y 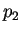
|
|
ice
2001-08-31
 ,
,  ,
, ![\includegraphics[width= 500pt]{capitulo4/ps/caso_4a.eps}](img841.gif)