Kari define el siguiente proceso para autómatas con ![]() ya que con estos podemos simular todo tipo de aut'omatas como se mostró en el capítulo 5 sección 5.2. Tomemos para ejemplificar este procedimiento el autómata reversible
ya que con estos podemos simular todo tipo de aut'omatas como se mostró en el capítulo 5 sección 5.2. Tomemos para ejemplificar este procedimiento el autómata reversible ![]() regla
regla ![]() .
.
Este autómata tiene como valores de sus índices de Welch, ![]() y
y ![]() ; debido a esto en la regla de evolución cada columna tiene una sola entrada para cada estado, es decir, cada columna es una permutación del conjunto
; debido a esto en la regla de evolución cada columna tiene una sola entrada para cada estado, es decir, cada columna es una permutación del conjunto ![]() . Esta cualidad, que siempre se presenta en este tipo de autómatas, Kari la aprovecha de la siguiente manera: sabemos que la regla de evolución
. Esta cualidad, que siempre se presenta en este tipo de autómatas, Kari la aprovecha de la siguiente manera: sabemos que la regla de evolución ![]() mapea vecindades a estados.
mapea vecindades a estados.
| (6.2) |
Por lo tanto, como en la regla de evolución cada columna tiene a todos los estados y estos parecen una sola vez cada uno, podemos definir la siguiente función.
| (6.3) |
Por ejemplo, el autómata ![]() regla
regla ![]() especificado en la Tabla 6.2 cumple que
especificado en la Tabla 6.2 cumple que ![]() por lo que
por lo que
![]() . Podemos extender esta definición para cadenas arbitrarias de elementos de la siguiente manera.
. Podemos extender esta definición para cadenas arbitrarias de elementos de la siguiente manera.
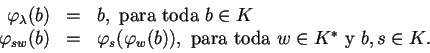 |
(6.4) |
En donde ![]() simboliza a la palabra vacía, así, retomando el autómata
simboliza a la palabra vacía, así, retomando el autómata ![]() regla
regla ![]() que se muestra en la Tabla 6.2, tenemos que:
que se muestra en la Tabla 6.2, tenemos que:
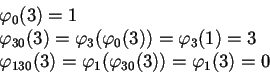
Usemos la función ![]() y definamos una jerarquía de relaciones
y definamos una jerarquía de relaciones
![]() de la siguiente forma:
de la siguiente forma:
| (6.5) |
Kari demuestra en [Kari 92] que las relaciones así definidas cumples con las siguientes propiedades:
Al número de clases de equivalencia distintas de ![]() lo denotaremos como
lo denotaremos como ![]() . Para
. Para ![]() tenemos que existen tantas clases de equivalencia como estados haya en el autómata o nodos en el diagrma de de Bruijn pues
tenemos que existen tantas clases de equivalencia como estados haya en el autómata o nodos en el diagrma de de Bruijn pues ![]() , es decir,
, es decir, ![]() . De las propiedades
. De las propiedades ![]() y
y ![]() , llegamos a que
, llegamos a que
![]() para toda
para toda ![]() , y
, y ![]() si
si ![]() . Así tenemos que en el peor caso
. Así tenemos que en el peor caso ![]() y que
y que
![]() , esto significa que en los ancestros de toda cadena de longitud menor o igual a
, esto significa que en los ancestros de toda cadena de longitud menor o igual a ![]() exiten tantas terminaciones derechas como
exiten tantas terminaciones derechas como ![]() y una única terminación izquierda, por lo que para esa cadena, ha quedado fijo un único elemento con el cual regresar hacia atrás en la evolución, concluyendo así que el máximo tamaño de la mínima vecindad inversa es
y una única terminación izquierda, por lo que para esa cadena, ha quedado fijo un único elemento con el cual regresar hacia atrás en la evolución, concluyendo así que el máximo tamaño de la mínima vecindad inversa es ![]() .
.
Utlizando el autómata ![]() de la Tabla 6.2, primero tomemos las
de la Tabla 6.2, primero tomemos las ![]() clases distintas que por definición existen para
clases distintas que por definición existen para ![]() , o sea, tomando la palabra vacía
, o sea, tomando la palabra vacía ![]() .
.
Formemos ahora las relaciones ![]() , observemos que para construir
, observemos que para construir ![]() , basta con revisar cada columna de la regla de evolución en la Tabla 6.2. Las columnas
, basta con revisar cada columna de la regla de evolución en la Tabla 6.2. Las columnas ![]() y
y ![]() son idénticas, por lo que estos elementos forman una única clase, las columnas
son idénticas, por lo que estos elementos forman una única clase, las columnas ![]() y
y ![]() siguen formando clases individuales.
siguen formando clases individuales.
Para obtener ![]() , se toman todas las cadenas de
, se toman todas las cadenas de ![]() elementos y sus ancestros:
elementos y sus ancestros:
Se observa en la Tabla 6.5 que en los ancestros de estas secuencias, los estados ![]() forman una sola clase ya que para toda cadena
forman una sola clase ya que para toda cadena ![]() , se tiene que
, se tiene que
![]() . Esto no ocurre con el estado
. Esto no ocurre con el estado ![]() , que sigue conservándose como una clase individual.
, que sigue conservándose como una clase individual.