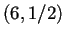 .
.
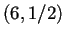 .
.
Tomemos al autómata reversible ![]() regla
regla
![]() .
.
Una evolución de este autómata se presenta a continuación.
Este autómata tiene índices de Welch con ![]() y
y ![]() ; veamos los ancestros de la cadena
; veamos los ancestros de la cadena ![]()
Para los ancestros de la Tabla 6.16 se tiene que el conjunto
![]() y
y ![]() ; también se cumple que existe un elemento de
; también se cumple que existe un elemento de ![]() que no se presenta en
que no se presenta en ![]() en este caso el nodo
en este caso el nodo ![]() . Formemos los ancestros de
. Formemos los ancestros de ![]() .
.
En la Tabla 6.17 se puede observar ahora que el conjunto
![]() con
con ![]() ; es decir, hubo un drecemento en el mínimo de alternativas internas.
; es decir, hubo un drecemento en el mínimo de alternativas internas.
Los ancestros de la secuencia ![]() son:
son:
En la Tabla 6.18 los ancestros de la secuencia ![]() muestran otro decremento en
muestran otro decremento en ![]() ; existen dos alternativas para el conjunto
; existen dos alternativas para el conjunto ![]() , ya sea
, ya sea
![]() o
o
![]() . Los ancestros de la secuencia
. Los ancestros de la secuencia ![]() se presentan en seguida.
se presentan en seguida.
La Tabla 6.19 expone que el valor de ![]() se conservó como estaba en la Tabla 6.18. Si tomamos a
se conservó como estaba en la Tabla 6.18. Si tomamos a
![]() se observa que para los demás conjuntos
se observa que para los demás conjuntos ![]() , con
, con
![]() e
e ![]() , los nodos de de Bruijn
, los nodos de de Bruijn ![]() se utilizan para hacer las
se utilizan para hacer las ![]() diferencias distintas de
diferencias distintas de ![]() con los demás conjuntos
con los demás conjuntos ![]() . Esto también se manifiesta si tomamos a
. Esto también se manifiesta si tomamos a ![]() o a
o a ![]() como
como ![]() .
.
Cualquier extensión que se haga de esta cadena debe ya presentar a ![]() pues el valor de de
pues el valor de de ![]() no se puede conservar por la longitud de la cadena, veamos estos ancestros.
no se puede conservar por la longitud de la cadena, veamos estos ancestros.
Cada una de las distintas familias de ancestros en la Tabla 6.20 muestran un único elemento en común, y los conjuntos ![]() y
y ![]() de cada familia son nodos de Welch izquierdo y derecho respectivamente. En el diagrama de de Bruijn los ancestros de la cadena
de cada familia son nodos de Welch izquierdo y derecho respectivamente. En el diagrama de de Bruijn los ancestros de la cadena ![]() tienen la presente construcción.
tienen la presente construcción.
La Figura 6.16 presenta ![]() nodos iniciales en el conjunto
nodos iniciales en el conjunto ![]() ,
, ![]() variantes internas en el conjunto
variantes internas en el conjunto ![]() y
y ![]() nodos finales con el conjunto
nodos finales con el conjunto ![]() . La ruta
. La ruta ![]() en el diagrama de subconjuntos tiene la siguiente forma.
en el diagrama de subconjuntos tiene la siguiente forma.
En la Figura 6.17 podemos ver que:
Las ![]() rutas representadas en la Figura 6.17 se constituyen en principio por
rutas representadas en la Figura 6.17 se constituyen en principio por ![]() nodos de de Bruijn, un mínimo de
nodos de de Bruijn, un mínimo de ![]() variantes internas y
variantes internas y ![]() nodos de de Bruijn finales.
nodos de de Bruijn finales.