 |
I have said that flexagons may be made with any number of sides. Surely, however, there is a limitation due to the bulkiness of the paper.
The situation is reminiscent of an old puzzle which requires that we fold a sheet of paper over, double, ten times. The puzzle can theoretically be solved, of course, but the bulk of paper involved would make the problem physically possible only through the use of a considerable yardage of extremely thin paper.
The practical limit for ordinary flexagons is somewhere around 50 sides. Many 48 sided straight-strip flexagons have been built successfully. However, by using a special type of flexagon and by omitting just about one-half of the different flexes that would ordinarily be possible, the practical limit may be extended quite appreciably. The only flexagon making use of this principle, a giant of 658 sides, is believed to hold the world's record. It is furthermore believed that the title will rest secure for some time, for the arduous chore of constructing such a monster will no doubt dissuade most contenders.
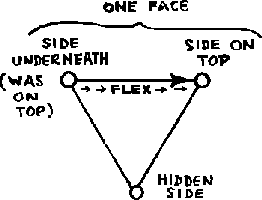
This large flexagon, it was said, makes usually half of the usual number of different flexes that would be used. What is this ``usual number?'' To find the answer to this problem, we again look to the map. On any map a line between two points represents the flexing operation that replaces the side represented by one of the two points with the side represented by the other point. That is, in passing along a map line, the point at the end of the line toward which we travel is the side that will next be found on top of the flexagon. The point we are leaving is the side that was last on top and which will next be found on the bottom. This is all diagrammed in figure 28. Now, it is possible to travel the other way along the same path, by turning the flexagon over. Therefore, each line connecting two points of the map stands for two different flexes and also for two different positions of the flexagon. We say that each path stands for two ``faces'' of the flexagon.
The number of faces, f, of a flexagon with n sides is given by the equation f =2(2n- 3) = 4n - 6.
To travel to every one of these faces in the shortest possible way, flex as long as possible without rotating, rotate, and so on, keeping this up until at least two sides repeat consecutively. Then turn the flexagon over and start again. This method takes 2(3n - 6) flexes and 2n rotations. It has been named the Tuckerman traverse after its inventor (L. B. Tuckerman).