Este modelo evoluciona en dos dimensiones con la vecindad de Moore, la regla de evolución es semitotalística y es representada como
![]() , recordemos que cuando una célula está viva se representa con el estado 1, si está muerta se representa con el estado 0. Las variables de la Ecuación 1 toman los valores de
, recordemos que cuando una célula está viva se representa con el estado 1, si está muerta se representa con el estado 0. Las variables de la Ecuación 1 toman los valores de ![]() ,
, ![]() ,
, ![]() y
y ![]() .
.
Conway hace un amplio análisis para poder determinar una regla de evolución que tuviera dos características fundamentales:
además se deben de definir tres condiciones, cuándo una célula debe de nacer, sobrevivir o morir. Estas condiciones son muy importantes para obtener las características mencionadas.
Por lo tanto la Equación 1 para la regla
![]() en particular queda como:
en particular queda como:
tenemos que
![]() es el intervalo de células vivas que originan un nacimiento de una célula que se encuentra muerta y
es el intervalo de células vivas que originan un nacimiento de una célula que se encuentra muerta y
![]() es el intervalo de células vivas que determinan la sobrevivencia de una célula que está viva. Las transformaciones para cada una de las células se efectúan de manera simultánea en el espacio de evoluciones.
es el intervalo de células vivas que determinan la sobrevivencia de una célula que está viva. Las transformaciones para cada una de las células se efectúan de manera simultánea en el espacio de evoluciones.
El interés que se originó en Life se debe principalmente a los comportamientos complejos que la regla de evolución puede producir, llegando a resultados muy importantes como fue el hecho de demostrar que Life puede realizar computación universal [BCG82].
En el espacio de evoluciones existen cuatro tipos de comportamientos característicos que se pueden obtener desde cualquier configuración aleatoria:
Las estructuras periódicas con desplazamientos conocidas como gliders son muy interesantes e importantes en Life. Muchos de los descubrimientos más relevantes están relacionados con este tipo de estructuras, determinando las trayectorias que pueden tener a través del espacio de evoluciones y que comportamientos o estructuras tan complejas se pueden llegar a producir cuando estos gliders colisionan entre sí o con otras estructuras.
El glider más relevante en la literatura de Life es el glider de cinco células ilustrado en la Figura 3, su periódo de desplazamiento es de dos células en cuatro generaciones.
El glider de la Figura 3 tiene una población total de cinco células y esta población se conserva en cada generación. Existen otros tipos de gliders que varían de forma, tamaño, periodo y dirección en el espacio de evoluciones, por lo tanto comportamientos de este tipo fueron los que originaron un interés más a fondo para poder explicar el origen y las construcciones de estas estructuras.
El glider gun ilustrado en la Figura 4 es una estructura que produce gliders como el de la Figura 3, de manera contínua cada treinta generaciones. Un descubrimiento muy importante y verdaderamente sorprendente realizado por Gosper, es que treinta gliders como el de la Figura 3 pueden construir su propio glider gun [BCG82], con este resultado se demostro que Life puede crecer ilimitadamente y puede reproducirse a sí mismo.
A continuación construimos el polinomio de la teoría del campo promedio paso a paso para ver con claridad la relación que existe entre las Ecuaciones 3 y 4. El número de combinaciones que se pueden generar en la vecindad de Moore cuando ![]() es igual a 28.
es igual a 28.
La Figura 5 ilustra las 28 combinaciones que se pueden generar en 8 células cuando ![]() , es decir, el número de vecindades cuando la célula central está viva y sus vecinos suman dos células vivas, para que en la siguiente generación la célula central permanezca viva.
, es decir, el número de vecindades cuando la célula central está viva y sus vecinos suman dos células vivas, para que en la siguiente generación la célula central permanezca viva.
Tenemos que ![]() y
y ![]() cuando
cuando ![]() , notemos que las combinaciones se realizan sobre los vecinos
, notemos que las combinaciones se realizan sobre los vecinos
![]() , donde la célula central
, donde la célula central
![]() es ocupada por el estado 1. En realidad al momento de calcular las combinaciones no importa si
es ocupada por el estado 1. En realidad al momento de calcular las combinaciones no importa si
![]() es ocupada por el estado 1 o el estado 0, sin embargo
es ocupada por el estado 1 o el estado 0, sin embargo
![]() es importante al momento de definir los exponentes del polinomio.
es importante al momento de definir los exponentes del polinomio.
Ahora se realiza el cálculo cuando ![]() .
.
En la Figura 6 se ilustran las 56 vecindades que se transforman al estado 1 en la siguiente generación cuando ![]() . De esta manera se calcula el número de combinaciones empleando el coeficiente binomial:
. De esta manera se calcula el número de combinaciones empleando el coeficiente binomial:
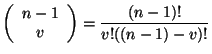 |
(7) |
donde
![]() y
y
![]() . Por ejemplo para el caso de la Figura 5 se tiene que
. Por ejemplo para el caso de la Figura 5 se tiene que ![]() y
y ![]() entonces:
entonces:
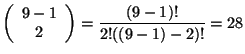 |
este número representa las combinaciones sin repetición que se generan cuando ![]() . En el caso de la Figura 6 cuando
. En el caso de la Figura 6 cuando ![]() tenemos que:
tenemos que:
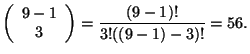 |
En el caso cuando ![]() y
y ![]() se tienen 56 combinaciones igual que cuando
se tienen 56 combinaciones igual que cuando ![]() y esto se debe porque las combinaciones se realizan en los vecinos
y esto se debe porque las combinaciones se realizan en los vecinos
![]() , es decir, las células de la vecindad sin tomar en cuenta la célula central
, es decir, las células de la vecindad sin tomar en cuenta la célula central
![]() . Por lo tanto las combinaciones de
. Por lo tanto las combinaciones de ![]() son iguales a las combinaciones de
son iguales a las combinaciones de ![]() y
y ![]() .
.
El grado del polinomio se determina por el número de células vivas ![]() y por el número de células muertas
y por el número de células muertas ![]() , que existen en los vecinos
, que existen en los vecinos
![]() . En el caso cuando
. En el caso cuando ![]() el exponente
el exponente ![]() y
y ![]() , cuando
, cuando ![]() el exponente
el exponente ![]() y
y ![]() , cuando
, cuando ![]() el exponente
el exponente ![]() y
y ![]() y cuando
y cuando ![]() el exponente
el exponente ![]() y
y ![]() .
.
Finalmente el polinomio para la regla de evolución Life queda como:
simplificando:
la probabilidad que genera cuando ![]() es la misma probabilidad cuando
es la misma probabilidad cuando ![]() , porque el número de 1's en la vecindad es igual en ambos casos, por esa razón se tienen tres términos en el polinomio de la Ecuación 8 en lugar de cuatro como pudiera pensarse.
, porque el número de 1's en la vecindad es igual en ambos casos, por esa razón se tienen tres términos en el polinomio de la Ecuación 8 en lugar de cuatro como pudiera pensarse.
La curva de probabilidad se obtiene poniendo el polinomio de la Ecuación 9 en términos de ![]() :
:
donde ![]() toma valores de 0 a 1. La curva de probabilidad del campo promedio muestra como se comporta la densidad de los estados en el espacio de evoluciones. La densidad es interpretada a través de la existencia de los puntos fijos en la curva de probabilidad que calcula el polinomio.
toma valores de 0 a 1. La curva de probabilidad del campo promedio muestra como se comporta la densidad de los estados en el espacio de evoluciones. La densidad es interpretada a través de la existencia de los puntos fijos en la curva de probabilidad que calcula el polinomio.
La gráfica de la Figura 7 muestra la curva de probabilidad que calcula el polinomio de la regla de evolución Life, el eje horizontal ![]() indica el valor al que será evaluado el polinomio, el eje vertical
indica el valor al que será evaluado el polinomio, el eje vertical ![]() indica el valor calculado, la función
indica el valor calculado, la función ![]() representa a
representa a ![]() , es decir, la probabilidad de obtener el estado 1 y es evaluado en el intervalo cerrado
, es decir, la probabilidad de obtener el estado 1 y es evaluado en el intervalo cerrado ![]() . La diagonal muestra los punto fijos al momento de intersectar algún punto de la curva con la diagonal, eso significa que
. La diagonal muestra los punto fijos al momento de intersectar algún punto de la curva con la diagonal, eso significa que ![]() en ese punto.
en ese punto.
El punto fijo estable que se encuentra en el origen de la gráfica indica que la probabilidad de tener 1's en la siguiente generación es cero, porque las vecindades a calcular tienen muy pocas células vivas. Además en el otro extremo del eje ![]() si el espacio de evoluciones tiene muchas células vivas, la probabilidad de tener 1's en la siguiente generación también es cero porque hay sobrepoblación.
si el espacio de evoluciones tiene muchas células vivas, la probabilidad de tener 1's en la siguiente generación también es cero porque hay sobrepoblación.
Existen dos puntos fijos más, un punto fijo inestable aproximadamente en 0.2 que indica la existencia de comportamientos impredecibles en el espacio de evoluciones, es decir, la densidad que existe en ese momento puede mantenerse igual, crecer o desaparecer por completo en pocas generaciones. El otro punto fijo es un punto crítico y se encuentra aproximadamente en 0.37 que indica la densidad promedio de células vivas que se mantienen vivas en el espacio de evoluciones a través del tiempo.
El análisis consiste en iterar el polinomio del campo promedio para ver como se comporta la curva de probabilidad en cada generación y de esta manera identificar el comportamiento de los estados a través del tiempo. Para obtener el comportamiento en la siguiente generación se sustituye el polinomio ![]() de la Ecuación 10, en él mismo para obtener la curva de probabilidad en
de la Ecuación 10, en él mismo para obtener la curva de probabilidad en ![]() de la siguente manera:
de la siguente manera:
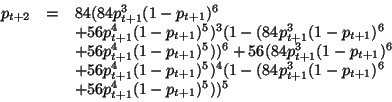
este polinomio calculara el comportamiento de la curva en la siguiente generación. Un problema es cuando se desean calcular más generaciones con los polinomios porque crecen exponencialmente, los polinomios para la tercera y cuarta generación ocuparían tres páginas completas.
En la Figura 8 se grafican las curvas de probabilidad para la segunda, tercera, cuarta y quinta generación de la regla de evolución Life. El comportamiento de las células en cada generación limita cada vez más su densidad en el espacio de evoluciones sobre el eje ![]() , en general éste es el comportamiento que debe seguir cualquier configuración inicial aleatoria en un largo tiempo.
, en general éste es el comportamiento que debe seguir cualquier configuración inicial aleatoria en un largo tiempo.
En la Figura 8 el intervalo de la curva sobre el eje ![]() se hace cada vez más estrecho, esto indica que la población de células vivas es cada vez menor y en efecto a sí ocurre en Life. La densidad promedio de 0.37 calculada para la regla de evolución Life, coincide con otros resultados obtenidos en [SS78] y [GV87]. Los demás casos de estudio analizados en este artículo se estudian de la misma manera, para posteriormente establecer una caracterización a través de sus curvas de probabilidad.
se hace cada vez más estrecho, esto indica que la población de células vivas es cada vez menor y en efecto a sí ocurre en Life. La densidad promedio de 0.37 calculada para la regla de evolución Life, coincide con otros resultados obtenidos en [SS78] y [GV87]. Los demás casos de estudio analizados en este artículo se estudian de la misma manera, para posteriormente establecer una caracterización a través de sus curvas de probabilidad.