As an interesting point, consider the proposition that a graph is the intersection of two copies of itself, yet the cartesian square or the tensor square of a diagram has quite a few more nodes. However they can be grouped into components, one single image of the graph repeated once for each node. A similar anomaly appears with the union of a graph with itself, both situations showing that the ordering is incompletely defined unless the role of functional mappings and equivalences is clearly understood.
To promote such an understanding, consider the cartesian product of the digon with itself. The nodes
![]()
are linked by
![]()
![]()
which are seen to form two independent digons; this is shown in Figure 3. Either of them can be mapped onto the original digon by one or another of various mappings, or the pair can be mapped in two to one fashion by either of the two coordinate projections.
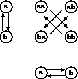
Figure 3: Greatest lower bound of a digon with itself.
Evidently graphs can have many representations, making it desirable to have ways of comparing them to one another; functional mappings among the nodes, which preserve linkage, provide a good mechanism.