![]()
Otra herramienta muy útil para el estudio de los AC es el diagrama de subconjuntos, que está estrechamente relacionado con el diagrama de Bruijn [8]. El diagrama de subconjuntos también es una gráfica dirigida, en la cual los vértices están etiquetados con los elementos de
![]()
donde S es el conjunto de secuencias
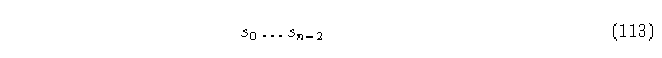
que etiquetan los vértices en el diagrama de Bruijn.
Las aristas en el diagrama de subconjuntos se colocan de acuerdo al siguiente criterio
a partir del diagrama de Bruijn, cuando el conjunto de estados tiene 2 elementos:
1.- Habiendo definido el conjunto potencia
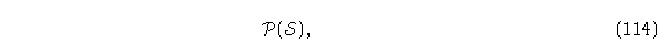
tomemos S como el vértice inicial.
2.- Ahora, sea S_0 el subconjunto de S cuyos elementos pueden ser
alcanzados desde cualquier elemento de S siguiendo una arista etiquetada con 0, y
sea S_1 el subconjunto de S cuyos elementos pueden ser alcanzados desde
cualquier elemento de S siguiendo una arista etiquetada con 1. Tomemos a S_0
y S_1 como siguiente nivel en el diagrama dibujando una arista etiquetada con 0
desde S a S_0 y otra arista etiquetada con 1 desde S hasta S_1
.
3.- Sea

el subconjunto de vértices que pueden ser alcanzados a partir de S_0 mediante una arista etiquetada con 0 en el diagrama de Bruijn, y

el subconjunto de vértices que pueden ser alcanzados siguiendo una arista etiquetada con 1 desde S_0 . Agreguemos estos subconjuntos a los vértices del diagrama de subconjuntos uniendo con una arista dirigida y etiquetada con 1 a los vértices S_0 a

De la misma manera unimos los vértices de S_1 a
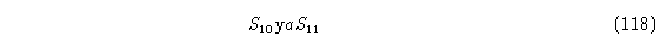
con una arista etiquetada con 1.
4.- Continuemos de esta manera, ahora tomando
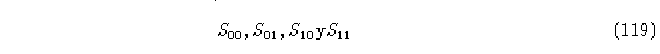
como subconjuntos iniciales. Continuemos hasta que ya no se generen nuevos
subconjuntos.
5.- Si siguiendo una arista etiquetada con un símbolo k que sale de cualquier subconjunto generado en éste proceso no se llega a ningún otro subconjunto, entonces esa arista se dirige al conjunto vacío
![]()
etiquetándola con k .
Una manera de nombrar a los subconjuntos es auxiliándonos de su representación en
base k . Así el conjunto vacío tiene el número 0 y el conjunto completo tiene el
número 15 como lo ilustra la siguiente tabla para AC (2,1):
Los subconjuntos se nombran por su equivalente decimal:

Teorema 6. Los AC lineales (2,1) con propiedades en la frontera izquierda y en la frontera derecha no tienen configuraciones jardines de edén.
Demostración.- Si f(X) es un AC como se definió en (7) entonces observando el diagrama de subconjuntos, del conjunto completo salen flechas que son autociclos, ésto es porque de acuerdo al diagrama de Bruijn, hay exactamente la mitad de flechas representando un estado, y la mitad de flechas que representan al otro estado. Dado que más de 2 flechas del mismo estado no pueden llegar al mismo vértice (teorema anterior), concluimos que llegan flechas de todos los estados a todos los vértices.
Ahora, si f(X) es como se definió en (8) de todos los vértices en el diagrama de Bruijn salen flechas que representan distintos estados por lo que los vértices
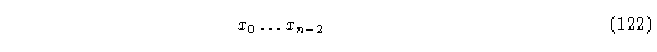
se unen por la derecha a otros vértices
![]()
y
![]()
y las vecindades
![]()
y
![]()
tienen diferentes mapeos en la función.
Puesto que no hay algún camino de cualquier longitud que conecte el conjunto completo
con el conjunto vacío, no existe configuración global alguna que sea jardín de edén q.e.d.
![]()