Para un AC lineal (k,r) donde n=2r+1, el diagrama de Bruijn es una gráfica dirigida y etiquetada, con 2n-1 vértices y 2n aristas. Los vértices se etiquetan con los dígitos binarios de los enteros desde 0 hasta
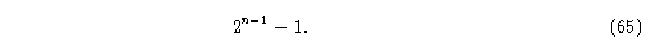
Un vértice está dirigido desde el vértice
al vértice
si y sólo si
tal que
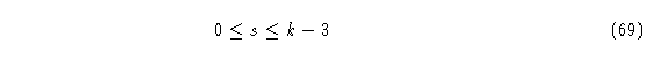
Lo que quiere decir que las secuencias de caracteres que definen los vértices i y j se traslapan en los dígitos s, y éste hecho lo denotaremos como
Cuando existe esta arista, se etiqueta con el resultado de aplicar la regla de evolución a
como se muestra en la figura 2.
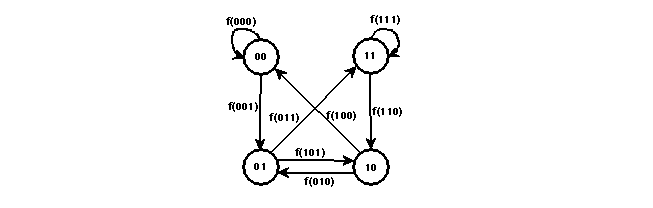
Figura 2: Diagrama de Bruijn genérico para AC lineales (2,1)
Una aplicación inmediata para éste tipo de diagramas, es dada una secuencia de
dígitos, encontrar otra secuencia que es preimagen de la primera.
Si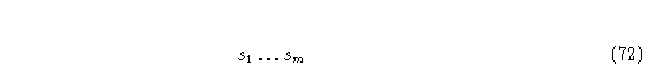 
es una secuencia binaria de m dígitos, se
puede encontrar un ancestro para esta secuencia buscando todos los caminos de longitud m
que se pueden encontrar a través de las aristas etiquetadas con
y construyendo las secuencias que se generan por el traslape de los n-1
vértices. Si no se puede hallar un camino, entonces esa secuencia no tiene preimagen y
constituye un ``jardín de edén''. Los diagramas de Bruijn nos indican todos los posibles
ancestros para una cadena de longitud n.
Para mostrar lo anterior, sea st = 1001010101011 la secuencia de dígitos de la cual deseamos conocer un ancestro, sea
la cadena buscada y
la regla de evolución clasificada con 60 bajo el criterio de Wolfram (siguiendo con la
regla expuesta en el ejemplo anterior).
Recordemos que en este diagrama, dos nodos que son conectados por una arista forman una secuencia y la etiqueta de la arista es el dígito que se genera, de esta manera para generar el primer dígito de la secuencia inicial s hay 4 posibilidades:
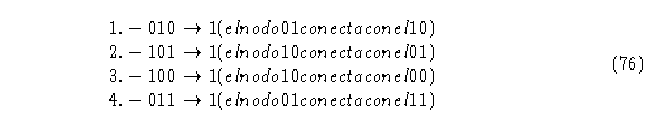
Para generar el segundo dígito en st que es un 0, de cualquier camino escogido anteriormente debemos seguir por una arista que esté etiquetada con 0. Esto elimina las posibilidades 1 y 2 ya que con estas no podemos seguir por una arista que esté etiquetada con un 0. Así que hasta ahora hemos generado 2 cadenas que son candidato para ser ancestro de st, la 100 y la 011, que llamaremos a y b respectivamente. Siguiendo por una arista etiquetada con 0 agregamos a la cadena s^(t-1) un 0 en el caso de a y un 1 en el caso de b, quedando formadas 1000 y 0111 respectivamente, Observamos que los nodos visitados son para el caso a:
En el paso 1 se genera la cadena 100, en el paso 2 la cadena 000 pero los 2 primeros 0's de esta cadena corresponden al traslape de las vecindades generadas en el paso 1 y el paso 2, así es de que sólo se agrega un dígito en cada paso, formando la cadena 1000; continuando hasta el paso 10 cuando se genera la cadena
El paso 11 también puede ser
de manera que
en el caso a puede ser a= 100011001100101 o bien a =
100011001100100. Para el caso b se procede de la misma manera, y los ancestros son b
= 011100110011010 o bien b = 011100110011011. En los AC con propiedades en la
frontera tanto en la izquierda como en la derecha, se observan algunas características
interesantes enunciadas en el siguiente teorema.
Teorema 2. En los AC(2,1) de izquierda con regla de evolución f definida como en (7), si
entonces a cada uno de los nodos del diagrama de Bruijn B , le llegan dos aristas una está etiquetada con e y la otra está etiquetada con 1-e . En los AC(2,1) de derecha con regla de evolución f definida como en (8), de cada uno de los nodos del diagrama de Bruijn B , salen 2 aristas una etiquetada con e y la otra etiquetada con 1-e.
Demostración.- Si
es como en (7), entonces
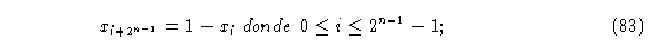
n=2r+1 . Pero cada vértice
en B recibe aristas de aquellos vértices etiquetados con
y
traslapándose para formar las vecindades
y
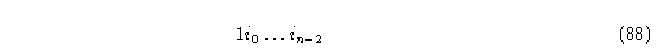
que producen símbolos diferentes bajo la regla de evolución f .
De manera similar, si
es como se definió en (8), entonces
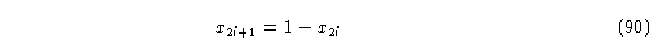
cuando
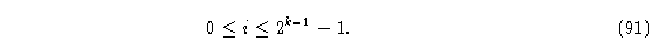
De cada vértice
salen aristas a vértices etiquetados con
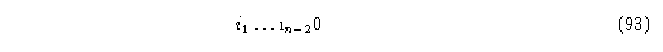
y
traslapándose para formar las vecindades
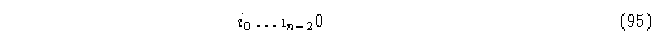
y
y por la definición de la función, estas vecindades generan símbolos diferentes q.e.d.
Ver figura 4.
Los diagramas de Bruijn para AC (k,r) tienen asociadas k matrices. En el caso (2,1) estas matrices se llaman matrices A y matriz B denotadas por B0 y B1 . En esta matriz, las filas y las columnas están etiquetadas con los símbolos de los nodos del diagrama de Bruijn y si i y j son nodos en el diagrama de Bruijn, entonces las entradas en la matriz serán un 1 si el nodo i se traslapa con el nodo j y además
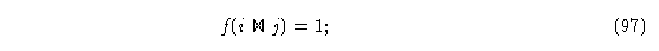
formando así la matriz de Bruijn A.
La matriz de Bruijn B se forma de manera similar, las entradas en la matriz B serán un 1 si el nodo i se traslapa con el nodo j y además
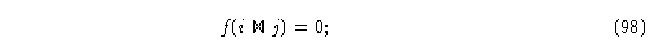
formando de esta manera la matriz de Bruijn B.
La suma de las k matrices (una para cada estado) genera la matriz topológica B
del diagrama de Bruijn. La cual podemos definir de la siguiente manera:
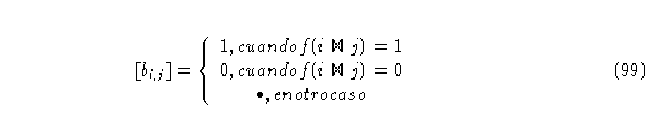
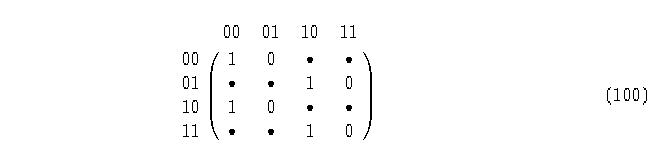
Matriz topológica de un AC(2,1)
Teorema 3. Si los elementos en las columnas de la matriz topológica definen una permutación de los estados y las entradas
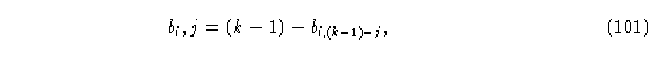
donde
es un elemento de B ; entonces la regla de evolución tiene propiedades de izquierda.
Demostración.-Supongamos que los elementos de cualquier columna en la matriz no son una permutación de los estados, lo cual significa que hay más de un renglón que en esa columna tiene la misma entrada. Supongamos ahora que la segunda condición tampoco se cumple, eso significa que la vecindad
puede tener el mismo mapeo en la función que la vecindad
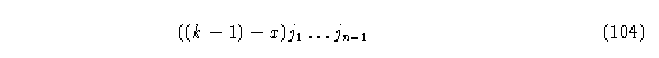
lo que contradice el enunciado. q.e.d.
Teorema 4. Si los elementos en las filas de la matriz topológica definen una permutación de los estados y
donde
es un elemento de B ; entonces la regla de evolución tiene propiedades de derecha.
Demostración.-Supongamos que los elementos de cualquier fila en la matriz no son una permutación de los estados, lo cual significa que hay más de una columna que en ese renglón tiene la misma entrada. Supongamos ahora que la segunda condición tampoco se cumple, eso significa que la vecindad
puede tener el mismo mapeo en la función que la vecindad
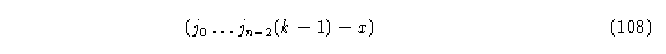
lo que de nuevo contradice el enunciado. q.e.d.
Teorema 5. El número de ancestros [10] de una secuencia
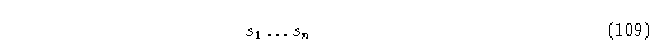
bajo un AC (k,r) está dado por la suma de los elementos en el producto:
En el caso de que el producto de (110) es igual a la matriz O la secuencia
no tiene ancestros en la regla f .
