![]()
Un AC lineal de k estados está definido de igual manera que un AC lineal de 2 estados, el par ordenado (k,r) indica un AC lineal de
![]()
y un radio de vecindad n=2r+1 ;
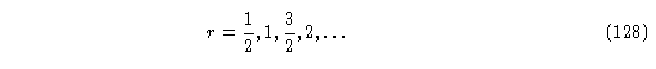
Cuando
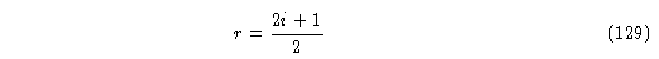
con i = 0,1,... se ajusta el valor de una célula entera a la izquierda o a la
derecha seleccionada arbitrariamente, por razones de simetría la célula nueva se coloca
debajo de la vecindad al centro de esta.
Las funciones que tienen propiedades de izquierda y de derecha como se definieron en (1) y (2) en el caso general se definen de la siguiente manera:
y
De manera similar a las definiciones (7) y (8) las reglas que tienen propiedades de izquierda y de derecha
tienen el mismo número de estados iguales.
Usando una definición de lógica multivaluada, en particular la negación de Lukasiewicz [9]. Otro resultado de lógica multivaluada es considerar la negación de una variable como neg(x) = x+1 (mod k) [9] que se conoce como negación cíclica. Con lo que la definición de AC con propiedades en la frontera se expresa como
y
En lo que resta del artículo, usaremos la primera definición, y tomaremos como
ejemplo el AC (4,h) . El valor h es una constante que significa 1/2, dicho
sea de paso, t es otra constante que significa 3/2.
En los (4,h) tenemos (2h+1)4 = 24 = 16 posibles configuraciones locales
diferentes, y 164 = 65536 reglas de evolución diferentes, como se puede observar,
el número de reglas crece de manera exponencial cuando crece el número de estados. Lo
que constituye un problema para etiquetar las reglas y es una razón para que en el
estudio de los AC el número de estados y el radio de la configuración local tipicamente
sea pequeño.
Cada una de las 16 configuraciones locales puede tomar 1 de 4 estados, los cuales
están nombrados de 0 a 3. Agrupamos las vecindades en conjuntos de 2 y nombramos con 0,1,
...,F a cada una de las combinaciones, que en base 4 tienen 2 dígitos los cuales
corresponden al estado que genera cada una de las 2 vecindades en el grupo. De manera que
la clave 1BD8721B representa la regla de evolución que se muestra en la tabla siguiente.
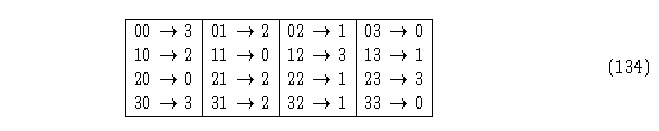
AC(4,h) Regla 1BD8721B
Ahora vamos a generalizar los resultados obtenidos en los teoremas 3 y 4, pero antes vamos a
generalizar la definición de la matriz topológica para un AC lineal de k estados
y vecindad n=2r+1 .
Si
![]()
y
![]()
son secuencias de n-1 dígitos, donde
![]()
la matriz topológica B del AC Lineal de k estados y una vecindad n se define como:

De esta manera, la clave 1BD8721B que representa la regla de evolución que se mostró anteriormente queda expresada en forma de matriz topológica de la siguiente manera:
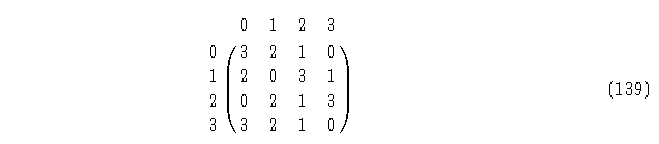
Matriz topológica del AC (4,h) Regla 1BD8721B
Teorema 7. Si en la matriz topológica de una regla de evolución de un AC(k,r), los elementos en los renglones son una permutación de los elementos en el conjunto de estados y las entradas
![]()
donde
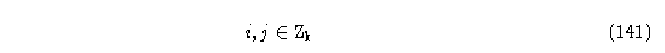
entonces la regla de evoluci\'on tiene propiedades de izquierda.
Demostración.- La matriz topológica es una matriz cuadrada de orden k
el hecho de que las entradas en cada renglón de cada columna sean una permutación del
conjunto de estados, hace que en cada renglón exista un elemento distinto a los demás.
Si en más de un renglón se encuentra la misma entrada, no se cumple la condición de la
función definida en (130). q.e.d.
Teorema 8. Si en la matriz topológica de una regla de evolución de un AC(k,r), los elementos en las columnas son una permutación de los elementos en el conjunto de estados y las entradas
![]()
donde
![]()
entonces la regla de evoluci\'on tiene propiedades de derecha.
Demostración.- De manera similar, la matriz topológica es una matriz cuadrada
de orden k el hecho de que las entradas en cada columna de cada renglón sean una
permutación del conjunto de estados, hace que en cada columna exista un elemento distinto
a los demás. Si en más de una columna se encuentra la misma entrada, no se cumple la
condición de la función definida en (131). q.e.d.
Teorema 9. Si una regla de evolución de un AC(k,r) tiene propiedades de izquierda, entonces en el diagrama de subconjuntos las flechas que llegan al conjunto vacío son autociclos. Demostración.- A partir del teorema 7 en la matriz topológica están representados todos los estados en cada renglón, lo que significa que las vecindades que empiezan con la secuencia
![]()
y terminan con cualquier secuencia que es etiqueta de cada columna, tiene una representación completa del espacio de estados definido por el autómata, por lo que significa para una célula específica con estado
![]()
una vecindad de tamaño 2r+1 que la genera. q.e.d.
Teorema 10. Si una regla de evolución de un AC(k,r) tiene propiedades de derecha, entonces en el diagrama de subconjuntos las flechas que salen del conjunto completo son autociclos.
Demostración.- De manera similar al teorema anterior, a partir del teorema 8 en la matriz topológica están representados todos los estados en cada columna, lo que significa que las vecindades que terminan con la secuencia
![]()
y empiezan con cualquier secuencia que son etiqueta de cada renglón, tiene una representación completa del espacio de estados definido por el autómata, por lo que quiere decir que para una célula específica con estado
![]()
una vecindad de tamaño 2r+1 que la genera. q.e.d.
El significado de los dos teoremas anteriores, el teorema 9
y el teorema 10 es que no hay alguna secuencia de
dígitos en el diagrama de subconjuntos tal que a través de las aristas que conectan cada
uno de los elementos en la secuencia, se pueda llegar del conjunto completo al conjunto
vacío, lo que nos hace concluir que en éste tipo de autómatas no hay configuraciones
globales que sean jardines de edén.
Al final del artículo se encontrarán ejemplos de algunas reglas de evolución
correspondientes a los AC con 4 estados y un radio de vecindad 1/2.
![]()