Esta medida de caos, fue introducida por el célebre matemático ruso Alexander Mijailovic Liapunov a principios del siglo XX, los exponentes de Liapunov, como ahora se les conoce, son un conjunto de números que se emplean usualmente para detectar la presencia del caos en sistemas dinámicos.
La idea en general es medir qué tan rápido se alejan o difieren las configuraciones globales contiguas con respecto al tiempo.
Figura 2: El mapa de retorno muestra las velocidades instantaneas en el punto de retorno de las trayectorias. El promedio de las velocidades indica el exponente característico de Liapunov.
El exponente característico de Liapunov está definido para una función dinámica F con una configuración inicial 
de acuerdo a la siguiente expresión:
Donde 
es el valor absoluto de la primera derivada de la n-ésima iteración de f a partir de 
[14]
En otras palabras, la expresión (1) es el máximo valor que alcanza el promedio del orden exponencial de la velocidad, con la cual las configuraciones globales se alejan (o se acercan) de sus configuraciones globales inmediatas siguientes. Después de n pasos en el tiempo.
Para comprender lo anterior y tener un punto de referencia, es necerario primero definir un espacio métrico que relacione dos configuraciones globales en base a una medida de distancia.
Como es definido en topología, un espacio métrico debe cumplir con tres condiciones [10] para cualesquiera tres puntos diferentes x,y,z en el mismo espacio de representación:
La distancia que separa un punto de él mismo es nula.
La distancia que separa a dos puntos distintos, es la misma sin importar el orden en que se tomen los puntos.
Obedece la desigualdad del triángulo.
Sea E el espacio de representación de todas las configuraciones globales de tamaño n. Con 
. Sea también 
, no es necesario que 
. Sea la medida de distancia:
El subíndice i se coloca en forma creciente desde -n hasta 0 y de izquierda a derecha sobre todas las células de la configuración global. Significa que la diferencia en el estado de las células del extremo derecho es más significativa para estimar la distancia.
La letra k denota la cardinalidad del conjunto de estados que definen al autómata celular. En el caso de un autómata binario, k=2.
Esta medida de distancia y esta definición de exponente de Liapunov presentan deficultades. En primer lugar, la definición (1) está expresada para funciones dinámicas de variable real de tipo 
.
Es posible aplicar la definición anterior usando la derivada de una función booleana, ya que la regla de evolución puede ser considerada como una función bivaluada, sin embargo en este documento no se aborda esta posibilidad.
La medida de distancia expresada anteriormente, también presenta dificultades, ya que la fracción 
es prácticamente 0 cuando x es mayor que 30, siendo que el espacio de evolución del autómata normalmente es de mucho más que 30 células.
Sin embargo se ha publicado otra definición que está más de acuerdo con los términos usados en la teoría de autómatas celulares con el fin de valorar el exponente característico de Liapunov [3]. Si la regla básica de la evolución de un autómata celular es:
Es decir, el estado que adquiera la célula 
en el paso de tiempo t es dependiente del estado que tengan un conjunto de células en un radio máximo de r células en el paso de tiempo anterior t-1. Ahora, después de T pasos de tiempo, la célula 
depende ahora de a lo más 2rT células de la configuración global inicial, como se muestra en la figura 3.
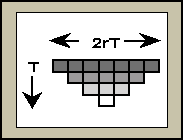
Figura 3: El estado de una célula en el tiempo T depende no sólo de su vecindad inmediata, sino de a lo más 2rT células en la configuración inicial
Lo que significa que, los patrones generados por la evolución del autómata se pueden propagar a velocidades mayores que r células por paso de tiempo debido a la correlación existente con las células vecinas y su dependencia con la vecindad que las generó. Aunque hay reglas que su velocidad de propagación de patrones es más lenta. En general, denotemos por 
a un número R que es el mínimo número de células que tienen influencia sobre el estado que una célula 
tome en el paso de tiempo T.
Entonces, la máxima velocidad de propagación asociada con la regla de evolución F es:
Sin embargo sólo se aplica a reglas simétricas, para las reglas que no son simétricas se pueden definir los exponentes característicos de Liapunov de izquierda y de derecha, denotados por 
y 
respectivamente.
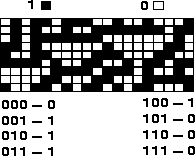
Figura 4: 8 generaciones a partir de una configuración global aleatoria bajo la regla de evolución 30 en un autómata celular lineal (2,1) con condiciones periodicas en las fronteras.
La figura 4 muestra una la evolución del autómata celular lineal (2,1) R30, durante 8 instantes de tiempo. Esta regla en especial muestra diferentes velocidades de transferencia de información, y se puede observar modificando ligeramente la configuración inicial.
La velocidad de transferencia, es el exponente de Liapunov, que es la velocidad con la que se ``separan'' las configuraciones globales, como lo ilustra la figura 5.
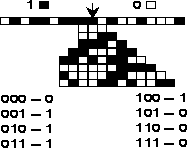
Figura 5: La velocidad de propagación de los patrones de diferencia que presenta la evolución al modificar una célula (señalada con una flecha) es diferente por ambos lados; por la derecha es 
y por la izquierda es 
Concluímos que el exponente de Liapunov puede ser:
En el primer caso, se verifica que la regla de evolución genera una velocidad de tranferencia positiva, es decir, se puede garantizar que al menos la distancia que separa dos configuraciones globales contiguas en el tiempo permanece constante. Si es así, la evolución tendrá más oportunidad de mostrar fases distintas a cada paso del tiempo; exhibiendo un comportamiento caótico.
Entonces, una regla de evolución tiene un comportamiento más caótico que otra, si el exponente característico de Liapunov de la primera regla de evolución es mayor que el de la segunda.
Aún se pueden verificar casos interesantes cuando el exponente de Liapunov es positivo:
se deduce de este valor un comportamiento esTabla, cada configuración global que es generada, dista de su configuración ancestra una medida constante, logrando ciclos atractores grandes (en dependencia del tamaño del espacio celular).
cuando ocurre esto la regla de evolución presenta un comportamiento caótico, y presenta esta característica más rápido a medida que el valor del exponente es mayor.
El segundo caso se puede interpretar como la existencia de un punto atractor, ya que la velocidad de transferencia disminuye a cada generación, lo que significa que a cada paso de tiempo la distancia entre dos configuraciones globales se reduce. Se esperaría que después de algunas evoluciones, el comportamiento global sea trivial.
