Es de mucha utilidad para caracterizar las reglas de evolución, saber el grado de caos de una fase de la evolución general de un autómata, desde el punto de vista topológico se puede definir la entropía espacial de conjunto como:
Donde el superíndice 
indica que se trata de secuencias espaciales de células, donde el tamaño de las secuencias es de X, 
es la probabilidad de que ocurra la secuencia en turno y 
es una función 
definida como:
si p = 0 y
en otro caso
Esta función 
cuenta el orden exponencial de todas las secuencias que es posible que ocurran.
A esta entropía espacial de conjunto también se le conoce como entropía topológica y va a compañada de una medida de entropía que se conoce también como métrica para la entropía, y está definida como sigue:
Para ilustrar el modo de operar de esta medida de entropía, así como la entropía espacial de conjunto, tómense bloques de tamaño 4 y sustitúyanse los valores correspondientes en las ecuaciones (8) y (9).
Hay que hacer notar que en la entropía espacial de conjunto lo que se observa es, en promedio, cuál es el orden exponencial de las ocurrencias de bloques de longitud X.
En el caso de la medida de entropía, lo observado es el promedio de la razón exponencial de que un bloque de longitud fija X aparezca en cualquier parte de la evolución de un autómata celular en un tiempo fijo t.
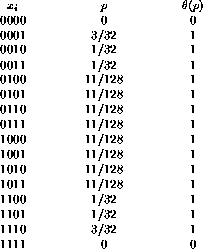
Tabla: Tabla que muestra todos los bloques de tamaño 4 con su probabilidad de ocurrencia y con la 
-evaluación. Nota:Los valores para las probabilidades se tomaron de manera arbitraria
En el ejemplo mostrado en la tabla 1, la entropía espacial de conjunto es:
Y la medida de entropía, tomando secuencias de células de tamaño 4 es:
Hemos de notar que el máximo valor de entropía se logra cuando todos los posibles 
bloques de longitud X tienen igual probabilidad de ocurrir. El máximo valor de entropía es 1.
Otro aspecto importante a la hora de asignar probabilidades de ocurrencia es que las secuencias que son ``Jardines de edén'' sólo ocurren una vez y jamás podrán aparecer de nuevo como imágen de una configuración global, así que la probabilidad de ocurrencia que le sea asignada debe ser muy pequeña si se empieza con una configuración aleatoria.
Ahora supóngase una configuración global 
al tiempo t de un autómata celular (2,1) de acuerdo a [8], en donde (k,r) indica que se trata de un autómata celular lineal de k estados y un radio de vecindad r, teniendo como vecindad un subconjunto de células contíguas de cardinalidad 2r+1.
= 1] 01011011000101011001 [0
Los dígitos a los extremos indican las condiciones periódicas de las fronteras.
Para calcular la entropía topológica de esta configuración, tomamos bloques de 3, ya que 3 es el número de células que interactúan como vecindad, para intervenir en la asignación de los estados para cualquier célula en transición, y aprovechando la facilidad de tomar secuencias de tamaño arbitrario.
De esta manera, en 
se tienen 18 bloques de longitud 3, distribuidas como sigue:
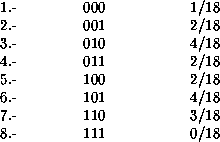
Que de acuerdo a (9)
...
Que muestra una medida de entropía aproximadamente de 0.8, lo que significa que en una medida razonable, aparecen todos los bloques de longitud 3, dentro de la configuración global 
.
En cambio, un valor de entropía bajo, indica que algunos bloques de tamaño X no aparecen, o la probabilidad de que aparezcan es muy pequeña.
