La expresión (2) calcula la aproximación del campo promedio para la regla general de un autómata celular, es decir una regla donde se declara de una manera explícita la asignación para cada una de las vecindades. Si se trata de un autómata celular (2,1) con la regla de evolución conocida como la regla 22 (estas dos útimas notaciones propuestas por Stephen Wolfram [9]) se tendrá una aproximación del campo promedio expresado por la siguiente función:
donde f(p) es la probabilidad de que aparezca el estado 1 en la siguiente generación y está determinado por la suma de las probabilidades de que ocurran las vecindades que lo originan.
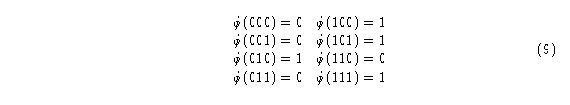
Regla de evolución general número 22
Sin embargo existen otras formas de realizar asignaciones en las vecindades, una de ellas es mediante la asignación de la transformación sobre (0,..,k-1) conjuntos de vecindades agrupados por alguna característica en común. La regla resultante de esta asignación llamada regla totalística, es especialmente útil si el número de vecindades es particularmente grande.
Cualquier función puede determinar la propiedad que caracterizará a los k-1 grupos, por ejemplo la suma de las células activas podría ser una de ellas. En nuestro caso tomaremos esta última por lo que considerando el mismo autómata celular (2,1) la asignación de una regla totalística sobre sus vecindades es:
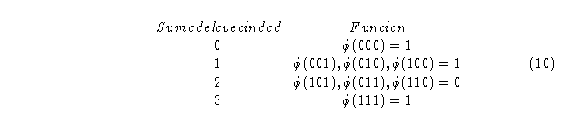
Los grupos resultantes son aquellos para los cuales la suma de sus células es 0,1,2 y 3 y el número de vecindades que conforman a cada grupo es de 1,3,3 y 1 respectivamente.
Para este caso la función del campo promedio es:
y la función que considera todos los grupos de vecindades posibles es:
como se puede observar los coeficientes de esta función están determinados por el número de vecindades que conforman a cada grupo. Y dado que cada grupo lo determina la suma de las células de la vecindad sin importar el orden en que se encuentren distribuidos los estados, los coeficientes se pueden calcular como:
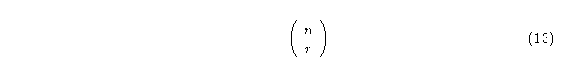
donde n es el tamaño de la vecindad y r es el número de estados que se suma.
De esta manera la función general que describe a la aproximación del campo promedio para las reglas totalísticas es:
La familia de polinomios que forma esta expresión son conocidas también como los polinomios de Bernstein (puntualmente los polinomios de Bernstein están expresados por prqn-r y la parte de la combinación calcula los coeficientes) y los coeficientes tienen relación con el triángulo de Pascal.
Si se considera un tamaño de la vecindad n=2 los coeficientes de la función son: 1,2,1si n=3 los coeficientes son: 1,3,3,1en general los coeficientes están relacionados con cada renglón del triángulo de Pascal, el primer renglón del triángulo determina los coeficientes para una vecindad de tamaño n=0, el segundo renglón lo hace para el tamaño n=1, el tercer renglón para n=2, etcétera, de manera que el triángulo de Pascal puede determinar los coeficientes para cualquier tamaño de vecindad como se muestra a continuación:
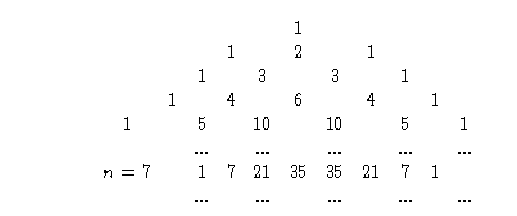
Triángulo de Pascal y las vecindades de tamaño n de un autómata celular.
De acuerdo al triángulo de Pascal los polinomios de Bernstein para los autómatas (2,3),(2,4),(2,5) y (2,6) son respectivamente:
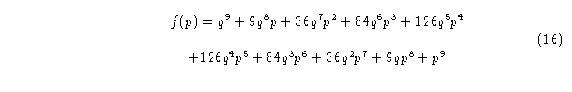
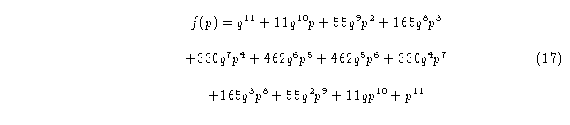
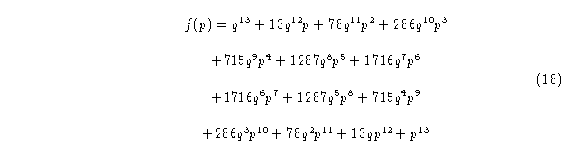
y
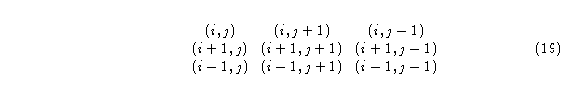
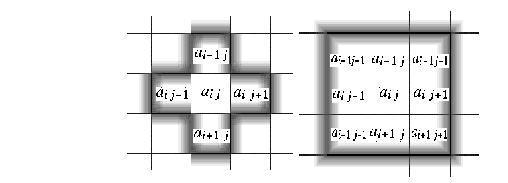
Figura 2: Vecindad de von Neumman y Moore de izquierda a derecha.
La asignación de 1's de la regla totalística determina que sumandos de su polinomio que podrán representarla. Esto se ya se ilustró con la formación de la expresión (11).