![]()
Johannes von Neumann [1] de origen húngaro era un verdadero genio en su tiempo, el encontro una importante relación entre las computadoras y los organismos naturales. Relaciono ambos sistemas encontrando características muy interesantes que dieron origen a una teoría que pudiera representar dichas propiedades. De esta manera von Neumann llama a su teoría, la Teoría de Autómata Celular. La teoría de autómata celular esta formada por un conjunto coherente de conceptos y principios enfocados a la estructura y organización de ambos sistemas, la programación y el control de tales sistemas. Von Neumann trabajó en el diseño de computadoras, programandolas para que reconocieran la lógica matemática y a su vez tuvieran un importante rendimiento en la nueva teoría de autómata celular, logrando de esta manera que la teoría de autómata celular fuera múltidiciplinaria. A grandes rasgos la naturaleza general de la teoría de autómata celular es su estructura, sus materiales, algunos de sus problemas, algunas de sus aplicaciones y la forma de su matemática; además von Neumann comenzo un estudio comparativo de autómata artificial y natural. Finalmente formuló un par de preguntas básicas en la teoría de autómata celular: ¿Como puedo construir sistemas confiables desde componentes no confiables?, ¿Qué tipo de organización lógica es suficiente para que un autómata sea capaz de auto-reproducirse?.
La idea de von Neumann, es que la matemática de la teoría de autómata celular debe empezar con la lógica matemática y moverse hacia un análisis, tal como la teoría de probabilidad y la termodinámica y cuando esto sea desarrollado, deberemos entender la gran complejidad del autómata celular, en particular el del sistema nervioso humano. El razonamiento matemático es ejecutado por el sistema nervioso humano y el lenguaje natural en que el razonamiento matemático toma su lugar es análogo para el lenguaje natural en el cómputo de la máquina. Esto es totalmente posible, en que la teoría de autómata celular debe ejecutar lógica y nuestros conceptos fundamentales de matemáticas. Ahora bien, la lógica es la base de las matemáticas; por lo tanto, si von Neumann dice que esto es verdad, la teoría de autómata celular debe moverse en forma circular, es decir, empezar en los fundamentos de las matemáticas y terminar ahí mismo.
Antes del estudio formal acerca de los autómatas celulares, surgieron otras teorías muy importantes que influyeron en los estudios de von Neumann, por ejemplo los estudios de Warren S. McCulloch y Walter Pitts sobre neurones (1943); una interesante abstracción matemática sobre expresiones regulares por S. C. Kleene (1951); los fundamentos generales de la cibernética introducida por Norbert Wiener (1948); por otra parte Henri Poincaré enfatizó en la cantidad de aspectos de la mécanica clásica en términos de estabilidad, propiedades ergódicas y la recurrencia de orbitas, tales temas actualmente constituyen una medida para estudios teóricos, topológicos y de dinámica simbólica, todo esto como resultado de las ideas de Poincaré; la dinámica simbólica elaborada por George Birkhoff y por último Gustav Adolf Hedlund [2] (1969) realizó un amplio trabajo que contiene abundantes resultados aplicables a la teoría de autómata celular, aunque este enfoque es totalmente diferente y la relación entre los dos conceptos no son por lo general bien apreciados [7].
Los autómatas celulares son una rama de la teoría de autómatas, la diferencia que existe entre estos es que los autómatas son manejados por señales de entrada que a su vez producen señales de salida. Los autómatas celulares por el contrario disfrutan de toda una simetría; sin embargo los autómatas celulares usan los estados de sus vecinos como señales de entrada y generalmente no producen señales de salida. La teoría de autómatas por si misma es bastante antigua, por un lado podemos ver que los autómatas son mecanismos capaces de ejecutar movimientos complejos y la teoría como tal comienza propiamente con la abstracción neurofisiológica de McCulloch y Pitts. Su fineza dentro de la teoría de expresiones regulares por Kleene, constituye uno de varios puntos de vista, donde término por incluir semigrupos (o monoides) de mapeos a un conjunto dentro de si mismo, que es justo la teoría de la gramática. La teoría de semigrupos es más compleja que la teoría de grupos, cuya clasificación sería una de las realizaciones matemáticas más importantes en los últimos tiempos y a su vez esta clasificación sería de gran utilidad para el estudio de los autómatas celulares. En las decadas de los 50's, 60's y 70's, se dieron grandes aportaciones en el estudio sobre autómatas, lenguajes y temas relacionados, pero a los autómatas celulares en particular no se les daría mucha atención.
El conocimiento público de los autómatas celulares puede ser atribuido enormemente a John Horton Conway. Interesado en buscar una simple configuración como la de von Neumann dio como resultado una serie de configuraciones para un autómata en dos dimensiones, que mostraban de manera muy ilustrativa y atractiva sus comportamientos a través del tiempo dentro de una lattice. Algunos de sus resultados fueron presentados en 1970 como un juego ecológico llamado Life, por Martin Gardner [3]. El juego de Life, sería el resultado de una regla muy particular, para un autómata celular en dos dimensiones (dos estados por célula), donde las vecindades estan formadas por una célula central y ocho más alrededor de esta, como se observa en la Figura 1.1. Conway examinó diferentes reglas para poder encontrar la regla que dio origen a su juego. Algunos de sus resultados más importantes fueron obtenidos en el Laboratorio de Inteligencia Artificial (MIT), con la ayuda de las facilidades gráficas de su computadora PDP-6.
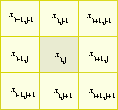
Figura 1.1: Vecindad de Moore.
En los últimos tiempos, la teoría de autómatas celulares recibio un considerable interés a través de las investigaciones de Stephen Wolfram [4], que emprendio un estudio computacional a través de las propiedades de los autómatas celulares en una dimensión; guiado por algunos conceptos de la dinámica no lineal y técnicas estadísticas. La idea del autómata celular en una dimensión es simple y su evolución a través del tiempo es ideal para una presentación en dos dimensiones. Para empezar hay una célula en una cierta región cada una en un punto dado, representados de diferentes formas llamados estados. Por conveniencia, estos estados son usualmente enumerados con pequeños valores, comenzando con cero hacia adelante. Para los propósitos de la teoría de autómatas celulares la naturaleza de los estados no importa ya que pueden ser representados de cualquier manera, lo que si es muy importante es su relación con los otros estados y el comportamiento de estos cambiando a través del tiempo y su medio ambiente.
Wolfram fue uno de los primeros en comparar las historias de evoluciones de un grán número de diferentes reglas para autómatas binarios, intentando su clasificación a través de su comportamiento en grandes evoluciones, surgiendo de esta manera las clases de Wolfram.
![]()