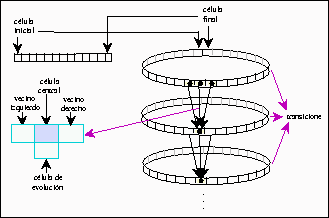
Figura 1.2: Estructura lineal de los autómatas celulares.
Wolfram por su parte describe algunos términos básicos para determinar su
clasificación de autómatas de acuerdo a su regla de evolución. Una tabla de
transiciones describe la función de mapeos en cada vecindad y esta función se denota
como 
. Para un autómata
celular su vecindad contiene 
vecindades por regla, que nos da un total de 
reglas de evolución. Por otra parte uno puede
tomar estados globales de la tabla de transiciones, es decir, el patrón de valores a
través de los renglones en el arreglo es el estado global del autómata celular en un
tiempo dado. Por lo tanto el autómata celular evoluciona a través de una sucesión de
estados globales (su trayectoria), además la iteración de su actualización global
produce la función de transición.
Dos tipos de autómata celular pueden ser distingidos, ambos determinísticos: el caso más general puede ser descrito teniendo grados de construcción desordenados, donde el diagrama dado y/o la función en cada célula pueden ser diferentes, como un ejemplo existen las redes de trabajo de funciones booleanas de Walker y las redes de trabajo booleanas de Kauffman. El autómata celular de construcción ordenada es un caso especial, donde el diagrama y la función son el mismo sobre todo el arreglo. En ocasiones, el orden puede ser confinado a una vecindad dentro de una zona ininterrumpida de células, típicamente centradas sobre la célula identificadora.