La teoría de registro de corrimientos es una disciplina basada en el tratamiento de secuencias translapando. Los nodos del diagrama de de Bruijn son secuencias de símbolos de algún alfabeto, justo como una expresión regular ya que ellos pueden ser secuencias de nodos de una gráfica específica, las ligas del diagrama describen como tales secuencias pueden translapar. Por consecuencia diferentes grados de translape conducen a diferentes diagramas.
Cuando los enteros son enteros consecutivos ellos pueden ser tratados como elementos de un anillo o quizás dentro de un campo finito y nos da la facilidad de discutir sus propiedades aritméticas o algebraicas, además de hacer varias elecciones valiosas. La matriz topológica del diagrama de de Bruijn se representa como:
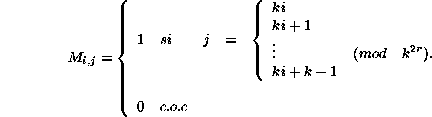
A través del diagrama de de Bruijn las gráficas pueden representar configuraciones o
clases de configuraciones en los autómatas celulares, las ligas del diagrama estan
naturalmente asociadas con las vecindades de un autómata usando los mismos símbolos que
asocian las ligas en un paso de evolución. Si hay alguna razón para descriminar entre
vecindades, la misma descriminación puede definir un subdiagrama del diagrama original.
El diagrama de de Bruijn genérico [8] para un
autómata 
, tiene cuatro nodos que corresponden a
cuatro vecindades parciales de dos células con ocho ligas representando todas las
vecindades de tres células.
La matriz topológica de un diagrama de de Bruijn es totalmente regular aunque es asimétrica y se diferencia de las matrices circulantes, matrices tridiagonales u otra forma especializada que haya sido extensamente analizada dentro de la literatura.
Figura 2.1: Diagrama de de Bruijn genérico para el autómata (2,1).
Las matrices de de Bruijn 
ó 
son caraterizadas por k, el número de
símbolos en que las secuencias pueden ser formadas y s el número de estados que
es la longitud de la secuencia.
En estos términos deben existir k ligas de entrada en cada nodo y k
ligas de salida en cada nodo, en total deben existir 
nodos con 
ligas uniendolos,
correspondiendo a las secuncias de longitud s+1.
Un buen ejemplo del uso de subdiagramas es el proceso conocido como naturaleza muerta, ya que estas son configuraciones de células que no cambian durante la evolución. El diagrama para la naturaleza muerta puede ser extraido del diagrama genérico removiendo todas las ligas que no conservan su célula central durante la evolución. Los ciclos en el subdiagrama contienen ligas que definen secuencias que son invariantes en la evolución, de esta manera toda la naturaleza muerta para el autómata es determinada automáticamente. En general, cualquier combinación booleana de las células de la vecindad y la célula de evolución pueden determinar el subdiagrama.
Figura 2.2: Subdiagrama de de Bruijn para un autómata (2,1).
Se hace resaltar de manera muy especial la importancia del uso de los diagramas de de Bruijn, ya que el significado del mismo diagrama no sólo representa el mapeo de las vecindades por su estado de evolución, si no que a través de estos diagramas y su respectiva matriz de evolución dan pie a la realización de otros diagramas tal como el diagrama de subconjuntos y el diagrama de parejas. Por otra parte su matriz de conectividad es de vital importancia para obtener una estimación del número de ancestros del mismo autómata.
Con esto se hace notar que la importancia de los diagramas de de Bruijn, es que estos
contienen en gran parte toda la información relevante que se quiera obtener del autómata
en estudio.