


Siguiente: Referencias
Arriba: Geometría Diferencial y Relatividad
Anterior: Conmutadores y desviaciones geodésicas
Sea 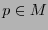 un punto en la variedad, y sea
un punto en la variedad, y sea  una métrica en el espacio tangente
una métrica en el espacio tangente 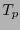 . En éste, consideraremos la base dada por las derivadas direccionales
. En éste, consideraremos la base dada por las derivadas direccionales
![$D=\left(\partial_i\right)_{i\in[\![0,n-1]\!]}$](img615.png) y en el cotangente
y en el cotangente 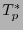 la base dada por las diferenciales
la base dada por las diferenciales
![$D^*=\left(\mbox{d}x_j\right)_{j\in[\![0,n-1]\!]}$](img617.png) , que es la base dual de la base de derivadas direccionales considerada en
, que es la base dual de la base de derivadas direccionales considerada en 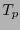 .
Se tiene que la base
.
Se tiene que la base 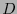 en
en 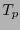 es ortonormal en el sentido de que
es ortonormal en el sentido de que
donde
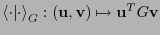 .
Sea
.
Sea
![$E=\left({\bf e}_i\right)_{i\in[\![0,n-1]\!]}$](img621.png) otra base de
otra base de 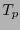 .
Expresemos a los elementos de la base inicial en términos de los de la nueva:
.
Expresemos a los elementos de la base inicial en términos de los de la nueva:
![$\partial_j = \sum_{i\in[\![0,n-1]\!]}e_{ij}{\bf e}_i$](img622.png) . Por la ortonormalidad de
. Por la ortonormalidad de 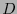 :
:
Por tanto, si denotamos por
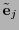 al vector columna de componentes
al vector columna de componentes 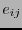 de
de  respecto a la base
respecto a la base  se tiene
se tiene
![\begin{displaymath}
\forall i,j\in[\![0,n-1]\!]:\ g_{ij} = \tilde{\bf e}_i^T H\tilde{\bf e}_j
\end{displaymath}](img627.png) |
(12.1) |
donde
Por la relación (12.1) se dice que 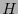 es el tensor raíz cuadrada de la métrica
es el tensor raíz cuadrada de la métrica  .
.
Sea
![$\tilde{E}=\left[\tilde{\bf e}_0\ \ \cdots\ \ \tilde{\bf e}_{n-1}\right]$](img629.png) la matriz cuyas columnas son los vectores columna
la matriz cuyas columnas son los vectores columna
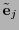 .
Sea ahora
.
Sea ahora
![$E^*=\left({\bf e}^*_i\right)_{i\in[\![0,n-1]\!]}$](img630.png) la base de
la base de 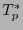 , dual de la base
, dual de la base  . Entonces
. Entonces
por tanto la matriz
![$\tilde{E^*}=\left(\overline{e}_{ij}\right)_{i,j\in[\![0,n-1]\!]}$](img633.png) que expresa a la base
que expresa a la base 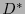 en términos de
en términos de  es tal que
es tal que
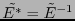 .
.
Si un vector
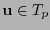 se expresa por los vectores columna
se expresa por los vectores columna
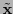 e
e
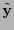 respecto a las bases
respecto a las bases 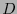 y
y  respectivamente, se tiene
respectivamente, se tiene
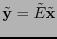 , en concordancia con (2.1).
Si
, en concordancia con (2.1).
Si
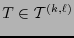 es un tensor, entonces sus componentes se cambian, respecto a las bases iniciales y a las nuevas, similarmente a (3.3).
es un tensor, entonces sus componentes se cambian, respecto a las bases iniciales y a las nuevas, similarmente a (3.3).
De manera general se puede suponer que los cambios de base están dados por transformaciones de Lorentz,  , o sea
, o sea 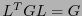 .
.
Sea 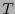 un
un  -tensor. Supongamos que el arreglo de componentes
-tensor. Supongamos que el arreglo de componentes
![$\left(T_{ij,k\ell}\right)_{i,j,k,\ell\in[\![0,n-1]\!]}$](img642.png) lo representa respecto a la base
lo representa respecto a la base
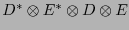 (es pues un tensor representado en una base mixta). Al representarlo respecto a
(es pues un tensor representado en una base mixta). Al representarlo respecto a
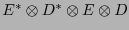 , las componentes se transforman, según (3.3), como:
, las componentes se transforman, según (3.3), como:
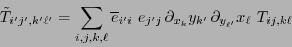 |
(12.2) |
Ahora bien, si
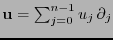 es un vector en
es un vector en  , de manera similar a (7.4) y (7.5), su derivada covariante es el
, de manera similar a (7.4) y (7.5), su derivada covariante es el  -tensor
-tensor
donde
![$M = \left[\mu_{ij}\right]_{i,j,k\in[\![0,n-1]\!]}$](img653.png) con
con
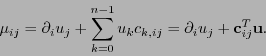 |
(12.4) |
Sea
![$\left(\omega_{i,jk}\right)_{i,j,k\in[\![0,n-1]\!]}$](img655.png) el arreglo de componentes del tensor de conexión respecto a la base
el arreglo de componentes del tensor de conexión respecto a la base
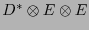 . Sea
. Sea 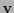 el vector columna que representa a
el vector columna que representa a
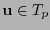 respecto a la base
respecto a la base  .
Al hacer el cambio de bases, resulta
.
Al hacer el cambio de bases, resulta
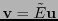 , y (12.4) queda:
, y (12.4) queda:
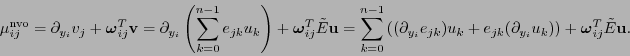 |
(12.5) |
Como
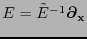 el análogo a (12.3) queda:
el análogo a (12.3) queda:
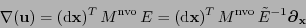 |
(12.6) |
donde
![$M^{\mbox{\scriptsize nvo}} = \left[\mu_{ij}^{\mbox{\scriptsize nvo}}\right]_{i,j,k\in[\![0,n-1]\!]}$](img661.png) . Comparando (12.6) con (12.3) se tiene
. Comparando (12.6) con (12.3) se tiene
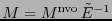 , y al comparar (12.5) con (12.4) se obtiene
, y al comparar (12.5) con (12.4) se obtiene
 |
(12.7) |
o equivalentemente
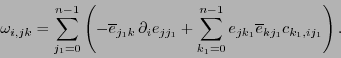 |
(12.8) |
Se tiene de aquí que vale el postulado de la cuarteta (debido a que fue planteado inicialmente en un espacio-tiempo de dimensión 4):
Si se pasa a una segunda base 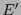 , al componer (12.8) (yendo de la base
, al componer (12.8) (yendo de la base 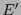 a
a 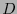 ) con (12.7) (yendo de la base
) con (12.7) (yendo de la base 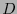 a
a  ) se tiene que el arreglo
) se tiene que el arreglo
![$\left(\omega'_{i,jk}\right)_{i,j,k\in[\![0,n-1]\!]}$](img667.png) de componentes del tensor de conexión respecto a la base
de componentes del tensor de conexión respecto a la base
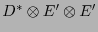 queda
queda
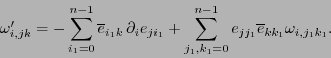 |
(12.9) |
Por otro lado, si 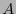 es un
es un 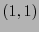 -tensor y el arreglo de coeficientes
-tensor y el arreglo de coeficientes
![$\left(a_{i,j}\right)_{i,j\in[\![0,n-1]\!]}$](img671.png) lo representa respecto a una base
lo representa respecto a una base 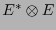 , entonces sus derivadas covariantes quedan expresadas como
, entonces sus derivadas covariantes quedan expresadas como
![\begin{displaymath}
\forall i,j,k\in[\![0,n-1]\!]:\ \nabla_i(a_{j,k}) = \partial...
...mega_{i,j\ell}a_{\ell,k} - \omega_{i,\ell k}a_{j,\ell} \right]
\end{displaymath}](img673.png) |
(12.10) |
El 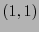 -tensor
-tensor 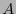 puede ser visto como una función lineal:
puede ser visto como una función lineal:
 |
(12.11) |
Como
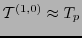 mediante una identificación natural, se tiene que (12.11) determina de hecho una aplicación lineal
mediante una identificación natural, se tiene que (12.11) determina de hecho una aplicación lineal 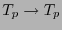 , una
, una 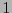 -forma vectorial. También
-forma vectorial. También  puede ser visto como la aplicación lineal:
puede ser visto como la aplicación lineal:
 |
(12.12) |
y ésta es de hecho una aplicación lineal
 , una
, una 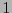 -forma funcional o covectorial.
-forma funcional o covectorial.
Similamente, si
![$A=\left(a_{ijk,\ell}\right)_{i,j,k,\ell\in[\![0,n-1]\!]}$](img679.png) es un arreglo que representa a un
es un arreglo que representa a un 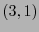 -tensor
-tensor 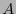 respecto a una base
respecto a una base
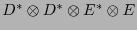 entonces éste determina una transformación lineal
entonces éste determina una transformación lineal
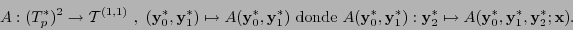 |
(12.13) |
Sea
 un
un 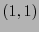 -tensor representado en la base
-tensor representado en la base 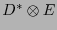 por el arreglo
por el arreglo
![$A=\left(a_{jk}\right)_{j,k\in[\![0,n-1]\!]}$](img685.png) y veámoslo como una
y veámoslo como una 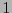 -forma vectorial según (12.11). Su derivada exterior, un
-forma vectorial según (12.11). Su derivada exterior, un 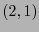 -tensor, debería tener componentes
-tensor, debería tener componentes
Por razones de homogeneidad en los tensores involucrados, consideremos para cada
![$k\in[\![0,n-1]\!]$](img687.png) el
el 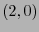 -tensor
-tensor
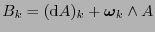 , con
, con
![$\mbox{\boldmath$\omega$}_k=\left(\omega_{i,kj}\right)_{i,j\in[\![0,n-1]\!]}$](img689.png) . De manera similar a (12.10), sus componentes han de ser
. De manera similar a (12.10), sus componentes han de ser
![\begin{displaymath}
\forall i,j\in[\![0,n-1]\!]:\ b_{ij,k} = \partial_ia_{jk} - ...
...mega_{i,k\ell}a_{j,\ell} - \omega_{j,k\ell}a_{i,\ell} \right].
\end{displaymath}](img690.png) |
(12.14) |
En particular, cuando  está dado por la matriz de cambio de base,
está dado por la matriz de cambio de base, 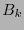 ha de coincidir con el tensor de torsión
ha de coincidir con el tensor de torsión
![$\mbox{\boldmath$\tau$}_k=\left(\tau_{ij,k}\right)_{i,j\in[\![0,n-1]\!]}$](img693.png) definido por (10.3):
definido por (10.3):
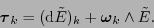 |
(12.15) |
Y si
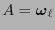 entonces
entonces 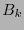 va a coincidir con el tensor de Riemann cuyas componentes están definidas por (10.2):
va a coincidir con el tensor de Riemann cuyas componentes están definidas por (10.2):
 |
(12.16) |
Las relaciones (12.15) y (12.17) se llaman ecuaciones estructurales de Maurer-Cartan.
También de (12.14) puede obtenerse las relaciones siguientes:
la última de las cuales es una generalización de las identidades de Bianchi (10.7).



Siguiente: Referencias
Arriba: Geometría Diferencial y Relatividad
Anterior: Conmutadores y desviaciones geodésicas
Guillermo M. Luna
2011-01-03
![]() un punto en la variedad, y sea
un punto en la variedad, y sea ![]() una métrica en el espacio tangente
una métrica en el espacio tangente ![]() . En éste, consideraremos la base dada por las derivadas direccionales
. En éste, consideraremos la base dada por las derivadas direccionales
![]() y en el cotangente
y en el cotangente ![]() la base dada por las diferenciales
la base dada por las diferenciales
![]() , que es la base dual de la base de derivadas direccionales considerada en
, que es la base dual de la base de derivadas direccionales considerada en ![]() .
Se tiene que la base
.
Se tiene que la base ![]() en
en ![]() es ortonormal en el sentido de que
es ortonormal en el sentido de que
![\begin{eqnarray*}
\forall i,j\in[\![0,n-1]\!]:\ g_{ij} &=& \left\langle \partial...
...left\langle {\bf e}_{k_0} \vert {\bf e}_{k_1} \right\rangle _G.
\end{eqnarray*}](img623.png)
![]() la matriz cuyas columnas son los vectores columna
la matriz cuyas columnas son los vectores columna
![]() .
Sea ahora
.
Sea ahora
![]() la base de
la base de ![]() , dual de la base
, dual de la base ![]() . Entonces
. Entonces
![]() se expresa por los vectores columna
se expresa por los vectores columna
![]() e
e
![]() respecto a las bases
respecto a las bases ![]() y
y ![]() respectivamente, se tiene
respectivamente, se tiene
![]() , en concordancia con (2.1).
Si
, en concordancia con (2.1).
Si
![]() es un tensor, entonces sus componentes se cambian, respecto a las bases iniciales y a las nuevas, similarmente a (3.3).
es un tensor, entonces sus componentes se cambian, respecto a las bases iniciales y a las nuevas, similarmente a (3.3).
![]() , o sea
, o sea ![]() .
.
![]() un
un ![]() -tensor. Supongamos que el arreglo de componentes
-tensor. Supongamos que el arreglo de componentes
![]() lo representa respecto a la base
lo representa respecto a la base
![]() (es pues un tensor representado en una base mixta). Al representarlo respecto a
(es pues un tensor representado en una base mixta). Al representarlo respecto a
![]() , las componentes se transforman, según (3.3), como:
, las componentes se transforman, según (3.3), como:
![]() es un
es un ![]() -tensor y el arreglo de coeficientes
-tensor y el arreglo de coeficientes
![]() lo representa respecto a una base
lo representa respecto a una base ![]() , entonces sus derivadas covariantes quedan expresadas como
, entonces sus derivadas covariantes quedan expresadas como
![]() es un arreglo que representa a un
es un arreglo que representa a un ![]() -tensor
-tensor ![]() respecto a una base
respecto a una base
![]() entonces éste determina una transformación lineal
entonces éste determina una transformación lineal
![]() un
un ![]() -tensor representado en la base
-tensor representado en la base ![]() por el arreglo
por el arreglo
![]() y veámoslo como una
y veámoslo como una ![]() -forma vectorial según (12.11). Su derivada exterior, un
-forma vectorial según (12.11). Su derivada exterior, un ![]() -tensor, debería tener componentes
-tensor, debería tener componentes