Fases en la regla 110

En el espacio de evoluciones de la regla 110 se pueden ver estructuras periódicas que son creadas de manera natural a través del tiempo, sin embargo existen gliders difíciles de obtener a partir de configuraciones aleatorias, algunos de ellos pueden ser obtenidos a través de choques muy precisos, por ejemplo el glider H, el glider gun o el Bbar8 [Jua02].

En [Mc99] y [JM01] se muestran con detalle la estructura de cada uno de los gliders, en este caso solo ilustraremos algunos que nos serán útiles. McIntosh denota a estos polígonos como Tn, donde $n$ indica el tamaño del triángulo y $n \in \mathbb{Z}^{+}$.

Primero describimos el espacio de evoluciones de la regla 110 que está constituido por dos tipos de triángulos rectángulos alfa-$\alpha$ y beta-$\beta$ como se ilustra en la Figura 1 para el caso de un T3.

Figura 1: Tipos de triángulos T3

Es claro que estos triángulos equilateros pueden cubrir el espacio de evoluciones sin violar la regla de evolución, en este caso el triángulo T3 beta es el fondo periódico que domina en el espacio de evoluciones llamado por Cook ``ether''. Aunque el espacio de evoluciones puede ser cubierto por cualquier Tn hasta un T4 de manera individual, en el caso donde $n>4$ solo es posible con combinaciones de ellos y mejor aún, cada uno de los gliders por sí mismos pueden cubrir el espacio de evoluciones como se puede ver en [JMS02].

El ether define propiedades importantes para toda estructura que existe en el espacio de evoluciones, veremos como el ether define cuatro fases como se ilustra en la Figura 2.

Figura 2: Fases del ether

Es importante notar que este T3 beta determinará las fases de cada uno de los gliders, así como su período y desplazamiento, aún de manera informal estas propiedades son presentadas en [Jua01].

Para determinar una configuración en particular se deben seguir cada una de las fases que representa el T3 beta y obtener una evolución donde cada una de las estructuras puedan ser representadas en una sola fase en dos tipos de alineación.

Figura 3: Período del ether

Se tienen cuatro fases periódicas del ether $11111000100110 - e(f1)$ (`e(f1)' indica fase uno del ether), $10001001101111 - e(f2)$, $10011011111000 - e(f3)$ y $10111110001001 - e(f4)$ como se ilustra en la Figura 3.

Si la configuración inicial es cubierta con la expresión $*e*$, tendremos el espacio de evoluciones cubierto de puro ether. Se puede ver que cualquiera de estas cuatro fases es una permutación de la misma cadena. El período del ether es de 14 células a la derecha en 7 generaciones.

El ether puede representar dos tipos de pendientes, que determinan la velocidad máxima negativa y positiva que puede tener una estructura periódica en el espacio de evoluciones como se ilustra en la Figura 4.

Se puede ver que el desplazamiento de estas pendientes siempre es de 2 células, para obtener los choques entre gliders hay que identificar los puntos de contacto donde los gliders puede interactuar con otras estructuras.

Figura 4: Dos tipos de pendientes producidas por el ether

Estos puntos de contacto van a estar determinados por el número de margenes pares $mp$ e impares $mi$ que tenga un glider en particular.

Entonces los puntos de contacto para un glider $g$ estan determinados por el número de margenes pares de su lado izquierdo y por el número de margenes impares de su lado derecho. Ambos margenes tienen una correspondencia biyectiva y la existencia de un punto de contacto en una parte implica la existencia de un punto que no es de contacto en su contraparte [Jua01].

Los margenes pares tienen una altura de 4 células, mientras que los margenes impares tienen una altura de 3 células. Con estas simples propiedades se puede determinar el desplazamiento de un glider $g$ que es determinado por la siguiente ecuación:

$$d_{g}=(2*mi)-(2*mp).$$ (4.1)

Toda estructura periódica tendrá un período definido por la cantidad de margenes pares e impares, por lo tanto el período de una estructura en particular esta derminado por:

$$p_{g}=(3*mi)+(4*mp)$$ (4.2)

finalmente un glider tendrá una velocidad de:

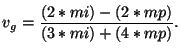$$v_{g} = \frac{(2*mi)-(2*mp)}{(3*mi)+(4*mp)}.$$ (4.3)

Para identificar algún glider en particular de la regla 110, utilizaremos la clasificación propuesta por Cook en [Cook99].

Analizemos el glider A y el glider B, el glider A tiene un margen impar, entonces tiene una velocidad de:

$v_{A} = \frac{(2*1)-(2*0)}{(3*1)+(4*0)} = \frac{2}{3}$

y un punto de contacto en su lado derecho. El glider B tiene un margen par y un punto de contacto en su lado izquierdo, entonces tiene una velocidad de:

$v_{B} = \frac{(2*0)-(2*1)}{(3*0)+(4*1)} = -\frac{2}{4} = -\frac{1}{2}$

se puede ver que ambos gliders tienen un punto que no es de contacto en su lado opuesto como se ilustra en la Figura 5.

Figura 5: Gliders A y B

Existe otro método para calcular el velocidad de un glider, como se hace en el Juego de la Vida de John Horton Conway [BCG82], la alternativa propuesta esta limitada a la regla 110. El cálculo para cada uno de los gliders existentes se describe con detalle en [Jua01].

Para determinar las fases que tiene un glider utilizamos la alineación del ether, cuando obtenemos una fase de manera implicita estamos calculando el número de margenes pares e impares y sus puntos de contacto, como se ilustra en las Figuras 5 y 6 para el glider A.

Figura 6: Fases del glider A

El glider A puede ser representado en 4 fases: $111110 - A(f1)$, $100011 - A(f2)$, $100110 - A(f3)$ y $101111 - A(f4)$. Cada una de ellas produce un glider de este tipo dejando el resto de la configuración en la fase correspondiente, se podrían utilizar combinaciones de ellas, pero el número de combinaciones crecería mucho, por esa razón utilizaremos solo una fase y veremos que con una de ellas es suficiente para obtener todos los choques deseados.

Analizemos la siguiente expresión:

$*e-A-e*$

el primer término indica que la parte izquierda de la configuración es cubierta por ether, en la parte central se encuentra un glider A y la parte derecha cubierta por ether, todas estas expresiones alineadas en fase uno del ether.

La principal razón por la que se utiliza una sola fase, es porque las cuatro fases son equivalentes.

Una manera de obtener estas secuencias es utilizando el diagrama de de Bruijn extendido [Mc91], donde el diagrama de de Bruijn calcula todas las secuencias periódicas representadas por los ciclos del diagrama. Una limitante es que para estructuras más elaboradas estos diagramas crecen exponencialmente.

Un estudio interesante en este camino puede ser estudiando los árboles topológicos que describe Andrew Wuensch en [WL92], identificando estructuras periódicas y sus ancestros en ciclos atractores, algo interesante es sobre la busqueda o representación de gliders en reglas de evolución con comportamiento complejo como puede verse en [Wue99].

Utilizando las fases del ether se pueden obtener todas las secuencias para una fase en particular de cualquier estructura periódica, en este análisis solo se toma en consideración un glider y no grupos de ellos o cualquier otra combinación, este problema es tratado en [JMS02].

Los puntos de contacto para los gliders son determinados por los margenes $mi$ y $mp$, pero a su vez estos margenes estan determinados por las fases del ether. Una vez identificados los puntos de contacto se realizó un estudio sistemático para calcular todos los choques binarios, esta colección se puede consultar en [JM01].

Los choques tienen una cota máxima que esta determinada por el número de margenes periódicos, entonces para un glider arbitrario con $mi$ puntos de contacto y otro glider arbitrario de $mp$ puntos de contacto, se tiene que:

$$c \leq \vert mi * mp\vert$$ (4.4)

donde $c$ representa el número máximo de choques que pueden existir entre dos gliders.

Sin embargo para algunos gliders que tienen puntos de contacto y de no contacto, la cota máxima no se cumple. Depurando la igualdad se tiene que el número de choques que existen entre dos gliders $g_{i}$ y $g_{j}$ esta representada por la siguiente ecuación:

$$c = \vert(mp_{g_{i}} * mi_{g_{j}}) - (mp_{g_{j}} * mi_{g_{i}})\vert.$$ (4.5)

Por ejemplo el glider Bbar tiene 3 margenes pares y 0 margenes impares, el glider G tiene 9 margenes pares y 2 margenes impares, recordemos que estos margenes siguen una correspondencia biyectiva y existen en igual cantidad en ambos lados de los gliders, entonces tenemos que:

$c = \vert(9 * 0) - (3 * 2)\vert = 6$

existen 6 maneras de chocar entre estos dos gliders como se ilustra en [JM01].

Un trabajo importante que trata de formalizar el número de choques entre gliders de manera general y no particular como en nuestro caso, puede ser consultado en el trabajo de Cosma Rohilla Shalizi [HSC01], donde los resultados obtenidos a través del estudio de mecánica computacional pueden ser aplicados en la regla 110.

Para dos gliders dados no todos los choques producen el fenómeno solitón, esto es originado por la fase en que chocan los gliders. Se tiene que controlar la fase en que los gliders llegan, la manera como controlamos estas fases es desde la configuración inicial.

Es recomendable dar un espacio entre los gliders para poder observar bien el choque, en algunas ocaciones no es necesario introducirlo ya que las cadenas estan alineadas a la fase del ether y esto produce siempre un choque propio.

Figura 7: Producción simétrica entre el glider G y Bbar

En la Figura 7 se puede ver el resultado de la expresión $*e-G(C2)-e-Bbar(C)-e*$, viene un glider Bbar en su fase 3 chocando con un glider G en su fase 11, el producto es la expresión $3A-D2-Bbar-F$ en orden de aparición³. El resultado es una producción simétrica compuesta de cuatro gliders y aunque el glider Bbar logra atravesar despues del choque el glider G no.

Finalmente esta es la manera para obtener los choques que son solitones, necesitamos saber en que fase se produce este fenómeno para los dos gliders en cuestión. Por ejemplo evaluemos la expresión $F(A2)-e-B$ que se sabe debe producir un solitón.

Figura 8: Solitón F $\rightarrow$ B

En la Figura 8 se puede ver un choque solitón entre el glider F y el glider B, donde los gliders conservan su forma y velocidad despues del choque, finalmente solo sufren un pequeño desplazamiento en sus fases, cumpliendo con las propiedades de un solitón.

En el universo de la regla 110 se pueden obtener solitones que viajen en la misma dirección, en direcciones opuestas o con un glider estático. Los desplazamientos en los gliders siempre se dan en retroceso al original, tal como ocurre en los solitones.

En el apéndice de este reporte mostramos todas las expresiones binarias que producen solitones con algunos de los gliders de la regla 110. Finalmente se puede decir que no todos los gliders pueden soportar solitones.