




Siguiente: Ejemplos de variedades diferenciables
Arriba: Aplicaciones de clase
Anterior: Caracterización de isomorfismos
Como ya observamos arriba, un espacio afín normado de dimensión infinita
no es una variedad diferenciable en el marco de nuestro libro. Podemos, sin embargo,
imitar la definición 5.3.1 y formular:
Definición 3.2
Sean  una variedad
una variedad  y
y  una aplicación de
una aplicación de  en un espacio
afín normado
en un espacio
afín normado  . Sea
. Sea
![$j \in [\![ 1, k ]\!]$](img4245.png) .
.  se dice APLICACIÓN DE CLASE
se dice APLICACIÓN DE CLASE  en M si
en M si
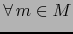 existe un mapa admisible
existe un mapa admisible  de
de  en el punto
en el punto  tal que la aplicación
tal que la aplicación
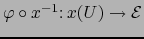 es de clase
es de clase  (C.D.) en el abierto
(C.D.) en el abierto 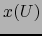 de
de
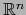 .
.
Teorema 3.8
Sean  una variedad
una variedad  y
y  una aplicación de
una aplicación de  en un espacio
afín normado
en un espacio
afín normado  . Sea
. Sea
![$j \in [\![ 1, k ]\!]$](img4245.png) . Si
. Si  es de clase
es de clase  en
en  , para todo mapa admisible
, para todo mapa admisible
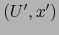 de
de  la aplicación
la aplicación
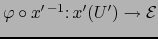 es
de clase
es
de clase  (C.D.) en
(C.D.) en
 .
.
Demostración
La demostración es parecida a la del teorema 5.3.1, pero más simple.
Supongamos la aplicación
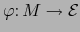 de clase
de clase  según la
definición 5.3.2. Sea
según la
definición 5.3.2. Sea
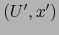 un mapa admisible arbitrario
de
un mapa admisible arbitrario
de  . Por el carácter local de aplicaciones de clase
. Por el carácter local de aplicaciones de clase  basta probar que
basta probar que
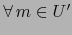 existe una vecindad abierta
existe una vecindad abierta 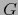 de
de  contenida en
contenida en
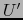 tal que la restricción de
tal que la restricción de
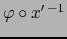 al abierto
al abierto
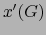 de
de
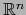 es de clase
es de clase  (C.D.).
(C.D.).
Sea, pues,  un punto arbitrario de
un punto arbitrario de 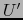 . Por hipótesis, existe un mapa
admisible
. Por hipótesis, existe un mapa
admisible  de
de  en el punto
en el punto  , tal que la aplicación
, tal que la aplicación
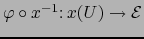 es de clase
es de clase  (C.D.) en
(C.D.) en 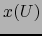 .
Restringiendo
.
Restringiendo
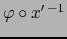 a
a
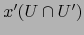 podemos
escribir:
podemos
escribir:
 |
(12) |
Ahora bien, el cambio de mapa
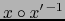 es de clase
es de clase  en
en
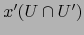 .
Manda este abierto de
.
Manda este abierto de
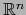 sobre el abierto
sobre el abierto
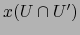 . Puesto
que
. Puesto
que
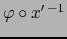 es de clase
es de clase  en
en
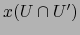 , se
sigue de (12) y del teorema 4.5.5, que
, se
sigue de (12) y del teorema 4.5.5, que
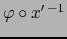 es de clase
es de clase
 en
en
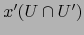 . Al tomar
. Al tomar
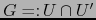 , nuestra
aserción está probada.
, nuestra
aserción está probada.






Siguiente: Ejemplos de variedades diferenciables
Arriba: Aplicaciones de clase
Anterior: Caracterización de isomorfismos
Guillermo M. Luna
2009-06-14
![]() de clase
de clase ![]() según la
definición 5.3.2. Sea
según la
definición 5.3.2. Sea
![]() un mapa admisible arbitrario
de
un mapa admisible arbitrario
de ![]() . Por el carácter local de aplicaciones de clase
. Por el carácter local de aplicaciones de clase ![]() basta probar que
basta probar que
![]() existe una vecindad abierta
existe una vecindad abierta ![]() de
de ![]() contenida en
contenida en
![]() tal que la restricción de
tal que la restricción de
![]() al abierto
al abierto
![]() de
de
![]() es de clase
es de clase ![]() (C.D.).
(C.D.).
![]() un punto arbitrario de
un punto arbitrario de ![]() . Por hipótesis, existe un mapa
admisible
. Por hipótesis, existe un mapa
admisible ![]() de
de ![]() en el punto
en el punto ![]() , tal que la aplicación
, tal que la aplicación
![]() es de clase
es de clase ![]() (C.D.) en
(C.D.) en ![]() .
Restringiendo
.
Restringiendo
![]() a
a
![]() podemos
escribir:
podemos
escribir: