




Siguiente: Aplicaciones de clase de
Arriba: Aplicaciones de clase
Anterior: Caracterización de mapas admisibles
Demostración
- Supongamos que
 es un isomorfismo
es un isomorfismo  de
de  sobre
sobre  .
.
Sea  un mapa admisible arbitrario de
un mapa admisible arbitrario de  . La hipótesis implica que
. La hipótesis implica que
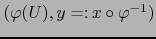 es un mapa admisible de
es un mapa admisible de  .
.
La aplicación  leída en dichos mapas es:
leída en dichos mapas es:
 |
(3) |
La aplicación 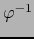 leída en los mismos mapas es:
leída en los mismos mapas es:
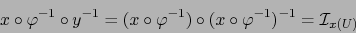 |
(4) |
Puesto que
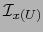 es de clase
es de clase  las relaciones (3) y (4)
muestran que
las relaciones (3) y (4)
muestran que
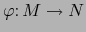 y
y
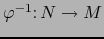 son de clase
son de clase
 .
.
- Recíprocamente supongamos que las aplicaciones
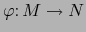 y
y
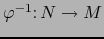 son de clase
son de clase  .
.
Sea  un mapa admisible arbitrario de
un mapa admisible arbitrario de  . Debemos probar que
. Debemos probar que
 es un mapa admisible de
es un mapa admisible de  . En virtud del
teorema 5.3.4, esto equivale a probar que las aplicaciones:
. En virtud del
teorema 5.3.4, esto equivale a probar que las aplicaciones:
son de clase  .
.
Ahora bien 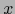 y
y 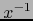 son de clase
son de clase  por el teorema 5.3.4
(o, si se prefiere, por los ejemplos 5.1 y 5.2).
por el teorema 5.3.4
(o, si se prefiere, por los ejemplos 5.1 y 5.2).  y
y 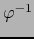 (y sus restricciones
a sendos abiertos
(y sus restricciones
a sendos abiertos 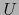 y
y  ) son de clase
) son de clase  por hipótesis. De ahí la conclusión por el teorema 5.3.2.
por hipótesis. De ahí la conclusión por el teorema 5.3.2.

Agregaremos a esta sección unos resultados relativos a productos de variedades.
Para terminar hablaremos de aplicaciones de clase  de variedades diferenciables
en espacios afines normados no necesariamente de dimensión finita.
de variedades diferenciables
en espacios afines normados no necesariamente de dimensión finita.
Lema 3.1
Sean 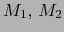 variedades
variedades  y sean
y sean
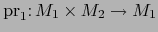 y
y
 las correspondientes proyecciones canónicas. Entonces
las correspondientes proyecciones canónicas. Entonces
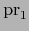 y
y
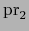 son aplicaciones de clase
son aplicaciones de clase  .
.
Demostración
Sea
 un punto arbitrario de
un punto arbitrario de
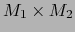 . Sean
. Sean
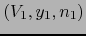 ,
,
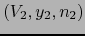 mapas admisibles de sendas variedades
mapas admisibles de sendas variedades 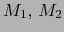 en sendos puntos
en sendos puntos
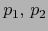 . Entonces
. Entonces
 es un mapa admisible
de
es un mapa admisible
de
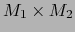 en el punto
en el punto  . La aplicación
. La aplicación
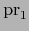 transforma
transforma
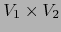 en
en
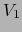 .
.
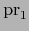 leída en los mapas
leída en los mapas
 y
y 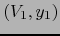 es:
es:
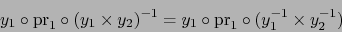 |
(5) |
Transforma todo punto
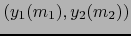 de
de
( ,
, 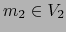 ) en
) en 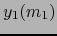 . Así pues, la aplicación (5) no es otra que la restricción al abierto
. Así pues, la aplicación (5) no es otra que la restricción al abierto
 de
de
 de
la proyección canónica
de
la proyección canónica
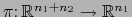 .
. 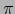 es de clase
es de clase
 . Luego
. Luego
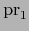 es de clase
es de clase  .
.
Asimismo, se demuestra que
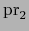 es de clase
es de clase  .
.

Teorema 3.7
Sean
 variedades
variedades  y sea
y sea  una aplicación
una aplicación
 .
.
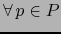 escribamos
escribamos
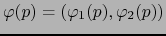 con
con
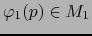 y
y
 o simplemente
o simplemente
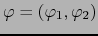 con
con
 y
y
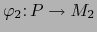 .
.
 es diferenciable en un punto
es diferenciable en un punto 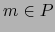 si y sólo si
si y sólo si 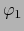 y
y
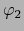 son diferenciables en
son diferenciables en  .
.
- Sea
![$j \in [\![ 1, k ]\!]$](img4245.png) .
.  es de clase
es de clase  en
en 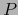 si y sólo si
si y sólo si
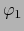 y
y 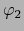 son clase
son clase  en
en 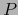 .
.
Demostración
- Vale:
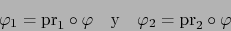 |
(6) |
- Supongamos
 es diferenciable en un punto
es diferenciable en un punto 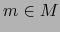 . Por el
lema 5.3.1 las aplicaciones
. Por el
lema 5.3.1 las aplicaciones
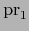 y
y
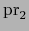 son de clase
son de clase  ; a fortiori
son diferenciables en el punto
; a fortiori
son diferenciables en el punto
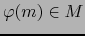 . En virtud del teorema 5.2.4,
las fórmulas (6) implican que
. En virtud del teorema 5.2.4,
las fórmulas (6) implican que 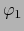 y
y 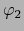 son diferenciables en el punto
son diferenciables en el punto
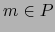 .
.
- Sea
![$j \in [\![ 1, k ]\!]$](img4245.png) . Supongamos que
. Supongamos que  es de clase
es de clase  en
en 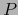 .
Ya que
.
Ya que
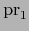 y
y
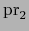 son de clase
son de clase  , son a fortiori de clase
, son a fortiori de clase  en
en  .
En virtud del teorema 5.3.2, las fórmulas (6) implican que
.
En virtud del teorema 5.3.2, las fórmulas (6) implican que 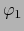 y
y 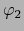 son de clase
son de clase  en
en 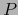 .
.
- Sea
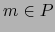 . Si
. Si 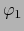 y
y 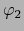 son de clase
son de clase  en
en 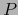 con algún
con algún
![$j \in [\![ 1, k ]\!]$](img4245.png) o si son meramente diferenciables en
o si son meramente diferenciables en  , son
continuas en
, son
continuas en  en virtud del teorema 5.2.2. Adoptemos por el momento cualquiera
de las dos hipótesis.
en virtud del teorema 5.2.2. Adoptemos por el momento cualquiera
de las dos hipótesis.
Sean
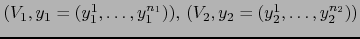 mapas admisibles
arbitrarios de sendas variedades
mapas admisibles
arbitrarios de sendas variedades 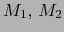 en sendos puntos
en sendos puntos 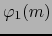 ,
,
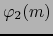 .
Luego
.
Luego
 es un mapa admisible de la variedad
es un mapa admisible de la variedad  en el punto
en el punto
 . Por continuidad
de
. Por continuidad
de 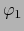 y
y 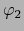 en
en  existen vecindades abiertas
existen vecindades abiertas 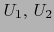 de
de  tales que
tales que
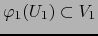 y
y
 . Cabe
suponer, por ejemplo, que
. Cabe
suponer, por ejemplo, que 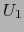 es dominio de un mapa admisible de
es dominio de un mapa admisible de 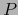 . Sea
. Sea
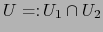 .
. 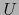 es dominio de un mapa admisibles
es dominio de un mapa admisibles  de la variedad
de la variedad 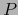 en
en  . Además
. Además
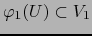 y
y
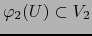 de donde
de donde
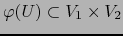 .
.
La aplicación 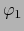 leída en los mapas
leída en los mapas  de
de  y
y
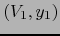 de
de 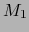 es:
es:
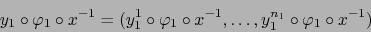 |
(7) |
La aplicación 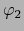 leída en los mapas
leída en los mapas  de
de 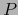 y
y 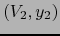 de
de 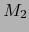 es
es
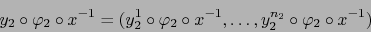 |
(8) |
A su vez, la aplicación  leída en los mapas
leída en los mapas  de
de 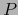 y
y
 de
de
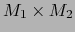 es:
es:
- Supongamos
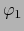 y
y 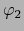 diferenciables en el punto
diferenciables en el punto 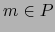 , o sea
las funciones
, o sea
las funciones
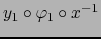 ,
,
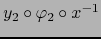 diferenciables C.D. en
el punto
diferenciables C.D. en
el punto 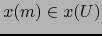 .
Por el teorema 4.4.1 y las fórmulas (8) y (9), son diferenciables C.D. en
.
Por el teorema 4.4.1 y las fórmulas (8) y (9), son diferenciables C.D. en  las funciones:
las funciones:
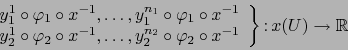 |
(10) |
Se sigue ahora de la fórmula (10) y del mismo teorema 4.4.1 que la aplicación
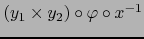 es diferenciable C.D. en el punto
es diferenciable C.D. en el punto  ,
o sea,
,
o sea,  es diferenciable en
es diferenciable en  .
.
- Finalmente, sea
![$j \in [\![ 1, k ]\!]$](img4245.png) y supongamos que las aplicaciones
y supongamos que las aplicaciones
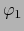 y
y 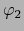 son de clase
son de clase  en
en 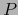 . Luego las aplicaciones:
. Luego las aplicaciones:
son de clase  (C.D.).
En virtud del teorema 4.5.2, las fórmulas (7) y (8) implican que las funciones (10)
son de clase
(C.D.).
En virtud del teorema 4.5.2, las fórmulas (7) y (8) implican que las funciones (10)
son de clase  (C.D.) en
(C.D.) en 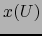 , luego por (9) y el mismo teorema 4.5.2, la aplicación:
, luego por (9) y el mismo teorema 4.5.2, la aplicación:
es de clase  (C.D.) en
(C.D.) en 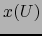 . Esto prueba que
. Esto prueba que  es de clase
es de clase  en
en 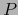 .
.

Corolario 3.1
Sean  ,
,  ,
, 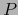 variedades
variedades  y sea
y sea
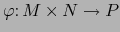 una aplicación
una aplicación  . Para todo punto
. Para todo punto 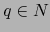 sea
sea
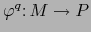 la
aplicación
la
aplicación
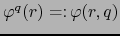
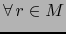 y para todo punto
y para todo punto 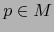 sea
sea
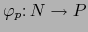 la aplicación
la aplicación

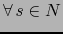 . Las aplicaciones
. Las aplicaciones
 y
y  (llamadas APLICACIONES PARCIALES de
(llamadas APLICACIONES PARCIALES de  ) son de
clase
) son de
clase  .
.
Demostración
Fijemos 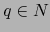 . Sea
. Sea
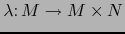 la aplicación:
la aplicación:
La aplicación 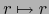 de
de  en sí, es la identidad de
en sí, es la identidad de  , luego es
de clase
, luego es
de clase  .
La aplicación
.
La aplicación 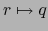 de
de  en
en  es constante, luego también es de clase
es constante, luego también es de clase
 .
Del teorema 5.3.7, se sigue que
.
Del teorema 5.3.7, se sigue que
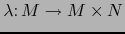 es de clase
es de clase  .
Pero
.
Pero
 |
(11) |
Por ser  y
y  de clase
de clase  , la fórmula (11) entraña que
, la fórmula (11) entraña que
 es de clase
es de clase  .
.
Análogamente se prueba que
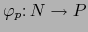 es de clase
es de clase  .
.

Corolario 3.2
Sean  ,
,  ,
, 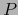 ,
, 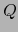 variedades
variedades  . Consideremos unas aplicaciones
. Consideremos unas aplicaciones
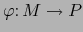 ,
,
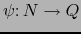 y la aplicación
y la aplicación
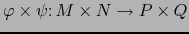 dada por
dada por
 o sea
o sea
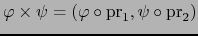 donde
donde
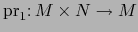 y
y
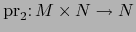 son las proyecciones canónicas.
son las proyecciones canónicas.
- Si
 y
y 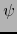 son diferenciables en sendos puntos
son diferenciables en sendos puntos 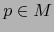 ,
,
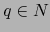 , la aplicación
, la aplicación
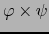 es diferenciable en el punto
es diferenciable en el punto
 .
.
- Si
 y
y 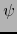 son de clase
son de clase  (
(
![$j \in [\![ 1, k ]\!]$](img4245.png) ), entonces la
aplicación
), entonces la
aplicación
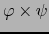 es de clase
es de clase  .
.
Demostración
Al suponer  diferenciable en el punto
diferenciable en el punto 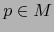 y
y 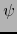 es diferenciable
en el punto
es diferenciable
en el punto 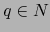 , para probar que
, para probar que
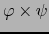 es diferenciable en el punto
es diferenciable en el punto
 , se debe probar, según el teorema 5.3.7, que las funciones
, se debe probar, según el teorema 5.3.7, que las funciones
 y
y
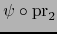 son diferenciables en el punto
son diferenciables en el punto 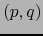 .
.
Al suponer  y
y 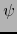 de clase
de clase  , para probar que
, para probar que
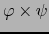 es de clase
es de clase  , se debe probar, según el teorema 5.3.7, que las funciones
, se debe probar, según el teorema 5.3.7, que las funciones
 y
y
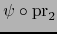 son de clase
son de clase  .
.
Ambas afirmaciones se siguen del lema 5.3.1 y del teorema 5.3.2.






Siguiente: Aplicaciones de clase de
Arriba: Aplicaciones de clase
Anterior: Caracterización de mapas admisibles
Guillermo M. Luna
2009-06-14
![]() será un isomorfismo
será un isomorfismo ![]() de
de ![]() sobre
sobre ![]() si
si
![]() y
y
![]() son aplicaciones de clase
son aplicaciones de clase ![]() .
.
![]() un mapa admisible arbitrario de
un mapa admisible arbitrario de ![]() . La hipótesis implica que
. La hipótesis implica que
![]() es un mapa admisible de
es un mapa admisible de ![]() .
.
![]() leída en dichos mapas es:
leída en dichos mapas es:
![]() un mapa admisible arbitrario de
un mapa admisible arbitrario de ![]() . Debemos probar que
. Debemos probar que
![]() es un mapa admisible de
es un mapa admisible de ![]() . En virtud del
teorema 5.3.4, esto equivale a probar que las aplicaciones:
. En virtud del
teorema 5.3.4, esto equivale a probar que las aplicaciones:
![]() y
y ![]() son de clase
son de clase ![]() por el teorema 5.3.4
(o, si se prefiere, por los ejemplos 5.1 y 5.2).
por el teorema 5.3.4
(o, si se prefiere, por los ejemplos 5.1 y 5.2). ![]() y
y ![]() (y sus restricciones
a sendos abiertos
(y sus restricciones
a sendos abiertos ![]() y
y ![]() ) son de clase
) son de clase ![]() por hipótesis. De ahí la conclusión por el teorema 5.3.2.
por hipótesis. De ahí la conclusión por el teorema 5.3.2.
![]()
![]() de variedades diferenciables
en espacios afines normados no necesariamente de dimensión finita.
de variedades diferenciables
en espacios afines normados no necesariamente de dimensión finita.
![]() un punto arbitrario de
un punto arbitrario de
![]() . Sean
. Sean
![]() ,
,
![]() mapas admisibles de sendas variedades
mapas admisibles de sendas variedades ![]() en sendos puntos
en sendos puntos
![]() . Entonces
. Entonces
![]() es un mapa admisible
de
es un mapa admisible
de
![]() en el punto
en el punto ![]() . La aplicación
. La aplicación
![]() transforma
transforma
![]() en
en
![]() .
.
![]() leída en los mapas
leída en los mapas
![]() y
y ![]() es:
es:
![]() es de clase
es de clase ![]() .
.
![]()
![]() mapas admisibles
arbitrarios de sendas variedades
mapas admisibles
arbitrarios de sendas variedades ![]() en sendos puntos
en sendos puntos ![]() ,
,
![]() .
Luego
.
Luego
![]() es un mapa admisible de la variedad
es un mapa admisible de la variedad ![]() en el punto
en el punto
![]() . Por continuidad
de
. Por continuidad
de ![]() y
y ![]() en
en ![]() existen vecindades abiertas
existen vecindades abiertas ![]() de
de ![]() tales que
tales que
![]() y
y
![]() . Cabe
suponer, por ejemplo, que
. Cabe
suponer, por ejemplo, que ![]() es dominio de un mapa admisible de
es dominio de un mapa admisible de ![]() . Sea
. Sea
![]() .
. ![]() es dominio de un mapa admisibles
es dominio de un mapa admisibles ![]() de la variedad
de la variedad ![]() en
en ![]() . Además
. Además
![]() y
y
![]() de donde
de donde
![]() .
.
![]() leída en los mapas
leída en los mapas ![]() de
de ![]() y
y
![]() de
de ![]() es:
es:
![]() . Sea
. Sea
![]() la aplicación:
la aplicación:
![]() es de clase
es de clase ![]() .
.
![]()
![]() diferenciable en el punto
diferenciable en el punto ![]() y
y ![]() es diferenciable
en el punto
es diferenciable
en el punto ![]() , para probar que
, para probar que
![]() es diferenciable en el punto
es diferenciable en el punto
![]() , se debe probar, según el teorema 5.3.7, que las funciones
, se debe probar, según el teorema 5.3.7, que las funciones
![]() y
y
![]() son diferenciables en el punto
son diferenciables en el punto ![]() .
.
![]() y
y ![]() de clase
de clase ![]() , para probar que
, para probar que
![]() es de clase
es de clase ![]() , se debe probar, según el teorema 5.3.7, que las funciones
, se debe probar, según el teorema 5.3.7, que las funciones
![]() y
y
![]() son de clase
son de clase ![]() .
.
![]()