Notaciones.
Sea
![]() . Sea
. Sea ![]() un punto interior de
un punto interior de ![]() .
.
![]() se llaman las DERIVADAS PARCIALES DE ORDEN
se llaman las DERIVADAS PARCIALES DE ORDEN ![]() de
de ![]() en
en ![]() con respecto
a la base
con respecto
a la base
![]() de
de ![]() .
.
En este libro nos será suficiente limitarnos al caso de ser ![]() de dimensión finita, en el cual podemos
contentarnos con una definición inspirada por el teorema 4.5.1.
de dimensión finita, en el cual podemos
contentarnos con una definición inspirada por el teorema 4.5.1.
Observación
Supongamos que también ![]() es de dimensión finita. Sea
es de dimensión finita. Sea
![]() un referencial
en
un referencial
en ![]() y sean
y sean
![]() las funciones coordenadas
de
las funciones coordenadas
de ![]() , con respecto a dicho referencial.
, con respecto a dicho referencial.
![]() será de clase
será de clase ![]() en
en ![]() si
si
![]() ,
,
![]() y
y
![]() existe en todo punto de
existe en todo punto de ![]() la derivada
la derivada
![]() y es continua en
y es continua en ![]() .
.
Aunque esta definición resulta a veces cómoda, no haremos uso de ella en lo que queda
de esta sección, donde supondremos en general
![]() , luego
, luego ![]() , pues
para nosotros ``
, pues
para nosotros ``![]() empieza con uno''.
empieza con uno''.
![]() es de clase
es de clase ![]() en
en ![]() si y sólo si
si y sólo si
![]() y
y
![]() existen en
existen en
![]() las derivadas parciales de orden
las derivadas parciales de orden ![]() :
:
![]() con respecto a la
base
con respecto a la
base
![]() de
de ![]() y son continuas en
y son continuas en ![]() .
.
Si además ![]() es de dimensión finita
es de dimensión finita ![]() y
y
![]() son las funciones
coordenadas de
son las funciones
coordenadas de ![]() con respecto a un referencial de
con respecto a un referencial de ![]() ,
, ![]() es de clase
es de clase ![]() en
en ![]() si y sólo si
si y sólo si
![]() la función
la función
![]() es de clase
es de clase ![]() en
en ![]() , es decir,
, es decir,
![]() y
y
![]() existen
en
existen
en ![]() las derivadas parciales
las derivadas parciales
![]() de orden
de orden ![]() en
en ![]() con respecto
a la base
con respecto
a la base
![]() de
de ![]() y son funciones continuas en
y son funciones continuas en ![]() .
.
Nota
Para evitar excursiones más profundas, e innecesarias en este libro, al cálculo diferencial, definimos aplicaciones de clase ![]() solamente
en el caso de ser el dominio
solamente
en el caso de ser el dominio ![]() de dichas funciones de dimensión finita. Por consiguiente, mantendremos esta hipótesis en todos los teoremas a continuación concernidos con
aplicaciones de clase
de dichas funciones de dimensión finita. Por consiguiente, mantendremos esta hipótesis en todos los teoremas a continuación concernidos con
aplicaciones de clase ![]() .
.
Demostración
Si
![]() es un referencial en
es un referencial en ![]() , vale por la fórmula (5), después de las
definiciones 4.1.6:
, vale por la fórmula (5), después de las
definiciones 4.1.6:
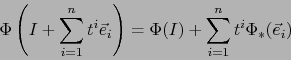
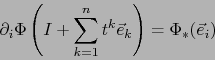
Si ![]() es un isomorfismo
es un isomorfismo ![]() de
de ![]() sobre
sobre ![]() y
y ![]() es un isomorfismo
es un isomorfismo ![]() de
de ![]() sobre
sobre ![]() , la aplicación compuesta
, la aplicación compuesta
![]() es un isomorfismo
es un isomorfismo ![]() de
de ![]() sobre
sobre ![]() .
.
Se supone que en cierto punto ![]() , la diferencial correspondiente
, la diferencial correspondiente ![]() es un isomorfismo lineal
de
es un isomorfismo lineal
de ![]() sobre
sobre ![]() . (Esta condición implica
. (Esta condición implica
![]() . En presencia de una base de
. En presencia de una base de ![]() y de un referencial en
y de un referencial en ![]() , dicha condición equivale a que el determinante de la
correspondiente matriz jacobiana de
, dicha condición equivale a que el determinante de la
correspondiente matriz jacobiana de ![]() en
en ![]() es distinto de cero).
es distinto de cero).
Entonces existe una vecindad abierta ![]() del punto
del punto ![]() , contenida en
, contenida en ![]() , tal que la restricción
de
, tal que la restricción
de ![]() a
a ![]() es un isomorfismo
es un isomorfismo ![]() de
de ![]() sobre un abierto
sobre un abierto
![]() de
de ![]() .
.
Recordemos que si ![]() son espacios topológicos, entonces una aplicación
son espacios topológicos, entonces una aplicación
![]() se
llama HOMEOMORFISMO LOCAL de
se
llama HOMEOMORFISMO LOCAL de ![]() en
en ![]() , si todo punto
, si todo punto ![]() posee vecindad abierta
posee vecindad abierta ![]() tal que la
restricción
tal que la
restricción ![]() es un homeomorfismo de
es un homeomorfismo de ![]() sobre un abierto
sobre un abierto ![]() de
de ![]() .
.
Todo homeomorfismo local
![]() es una aplicación abierta.
es una aplicación abierta.
En efecto, sea ![]() un abierto de
un abierto de ![]() y
y
![]() sea
sea ![]() una vecindad abierta de
una vecindad abierta de ![]() en
en ![]() tal que la restricción
tal que la restricción
![]() es un homeomorfismo de
es un homeomorfismo de ![]() sobre un abierto
sobre un abierto ![]() de
de ![]() . Vale
. Vale
![]() .
Ya que
.
Ya que
![]() el conjunto
el conjunto
![]() es abierto en
es abierto en ![]() se sigue que
se sigue que
![]() es abierto en
es abierto en ![]() .
.
He aquí un criterio muy usado para que una aplicación sea un isomorfismo ![]() .
.
Si además ![]() es una aplicación inyectiva,
es una aplicación inyectiva, ![]() es un isomorfismo
es un isomorfismo ![]() del abierto
del abierto
![]() de
de ![]() sobre el abierto
sobre el abierto
![]() de
de ![]() .
.
Demostración
Puesto que
![]() , la diferencial
, la diferencial ![]() es un isomorfismo lineal de
es un isomorfismo lineal de ![]() sobre
sobre ![]() , en virtud del
teorema 4.5.10, todo punto
, en virtud del
teorema 4.5.10, todo punto ![]() posee una vecindad abierta
posee una vecindad abierta ![]() contenida en
contenida en ![]() tal que
la restricción de
tal que
la restricción de ![]() a
a ![]() es un isomorfismo
es un isomorfismo ![]() , a fortiori un homeomorfismo
local de
, a fortiori un homeomorfismo
local de ![]() en
en ![]() y, por lo tanto, es una aplicación abierta de
y, por lo tanto, es una aplicación abierta de ![]() en
en ![]() . En particular
el conjunto
. En particular
el conjunto
![]() en abierto en
en abierto en ![]() .
.
Supongamos que, además, ![]() es una aplicación inyectiva. Podemos, pues, considerar
es una aplicación inyectiva. Podemos, pues, considerar
![]() como una biyección del abierto
como una biyección del abierto ![]() de
de ![]() sobre el abierto
sobre el abierto
![]() de
de ![]() .
Por hipótesis
.
Por hipótesis ![]() es de clase
es de clase ![]() en
en ![]() . Por el teorema 4.5.10,
. Por el teorema 4.5.10,
![]() la
restricción de
la
restricción de ![]() al abierto
al abierto ![]() es (un isomorfismo) de clase
es (un isomorfismo) de clase ![]() .
.
Ya que
![]() , por el teorema 4.5.6 (``carácter local
de las aplicaciones de clase
, por el teorema 4.5.6 (``carácter local
de las aplicaciones de clase ![]() ''), la aplicación
''), la aplicación ![]() es de clase
es de clase ![]() en el abierto
en el abierto
![]() .
.
De ahí concluimos que ![]() es un isomorfismo
es un isomorfismo ![]() del abierto
del abierto ![]() de
de ![]() sobre el abierto
sobre el abierto
![]() de
de ![]() .
.
![]()
Un contraejemplo
El simple contraejemplo a continuación muestra que la inyectividad de ![]() no es una consecuencia de las demás hipótesis del teorema 4.5.7, aunque unos
viejos autores ``hacían como si lo creyesen''.
no es una consecuencia de las demás hipótesis del teorema 4.5.7, aunque unos
viejos autores ``hacían como si lo creyesen''.
Sea
![]() la aplicación:
la aplicación:
